| Cálculo Diferencial e Integral 3 |
 cie
cieSeja 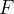 um campo vetorial
um campo vetorial
![\[ \mathbf{F}(x,y,z)=M(x,y,z)\mathbf{i}+N\left( x,y,z\right) \mathbf{j}+P\left( x,y,z\right) \mathbf{k} \]](images/img-1224.png) |
com  e
e 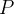 funções escalares cont
funções escalares cont nuas.
nuas.
Integral de fluxo de 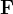 sobre
sobre 
 onde
onde  é o vetor normal unitário a
é o vetor normal unitário a  no ponto
no ponto 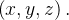 Supomos que os componentes de
Supomos que os componentes de 
 são funções cont
são funções cont nuas de
nuas de  e
e 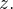 Se
Se  é o gráfico de uma equação
é o gráfico de uma equação
![\[ z=f\left( x,y\right) \]](images/img-1229.png) |
e fazemos 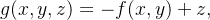 então
então  é também o gráfico de
é também o gráfico de
![\[ g(x,y,z)=0. \]](images/img-1231.png) |
Como 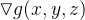 é o vetor normal ao gráfico de
é o vetor normal ao gráfico de  no ponto
no ponto  então
então
![\[ \mathbf{\eta =}\frac{\triangledown g(x,y,z)}{\left\Vert \triangledown g(x,y,z)\right\Vert }=\frac{-f_{x}(x,y)\mathbf{i}-f_{y}\left( x,y\right) \mathbf{j}+\mathbf{k}}{\sqrt{1+f_{x}\left( x,y\right) ^{2}+f_{y}\left( x,y\right) ^{2}}}. \]](images/img-1234.png) |
Analogamente, há fórmulas como estas no caso em que  é dado por
é dado por 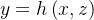 ou por
ou por 
Uma superf cie
cie  é orientada
é orientada 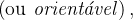 se existe um vetor unitário normal
se existe um vetor unitário normal  em cada ponto
em cada ponto  (não fronteira) e que as componentes de
(não fronteira) e que as componentes de  são funções cont
são funções cont nuas de
nuas de 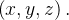 (
( varia continuamente sobre a superf
varia continuamente sobre a superf cie
cie  ). Admitamos também que
). Admitamos também que  tem também dois lados: o lado de cima e o lado de baixo do gráfico de
tem também dois lados: o lado de cima e o lado de baixo do gráfico de 
Volume do prisma de área  e altura
e altura 
![\[ dV=A.h=dS\left( \mathbf{F}\cdot \mathbf{\eta }\right) \]](images/img-1241.png) |
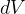 é a quantidade de fluido que atravessa
é a quantidade de fluido que atravessa  por unidade de tempo. Assim
por unidade de tempo. Assim
![\[ V={\displaystyle \iint \limits _{S}} \mathbf{F}\cdot \mathbf{\eta }\text { }dS \]](images/img-1243.png) |
é o volume total do flu do que atravessa
do que atravessa  por unidade de tempo.
por unidade de tempo.  é o fluxo de
é o fluxo de 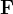 através de
através de 
Definição: Fluxo do campo vetorial 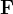 que atravessa
que atravessa 
![\[ {\displaystyle \iint \limits _{S}} \mathbf{F}\cdot \mathbf{\eta }\text { }dS \]](images/img-1244.png) |
e
![\[ m={\displaystyle \iint \limits _{S}} \delta (x,y,z)\mathbf{F}\cdot \mathbf{\eta }\text { }dS \]](images/img-1245.png) |
é a massa do flu do que atravessa
do que atravessa 
Exemplo: Seja  a parte do gráfico de
a parte do gráfico de 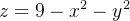 com
com  Se
Se  ache o fluxo de
ache o fluxo de 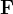 através de
através de 
Solução: Consideremos
![\[ g(x,y,z)=z-9+x^{2}+y^{2}=0 \]](images/img-1249.png) |
da
![\[ \mathbf{\eta =}\frac{\triangledown g}{\left\Vert \triangledown g\right\Vert }=\frac{2x\mathbf{i}+2y\mathbf{j}+\mathbf{k}}{\sqrt{1+4x^{2}+4y^{2}}} \]](images/img-1250.png) |
logo
![\[ {\displaystyle \iint \limits _{S}} \mathbf{F}\cdot \mathbf{\eta }\text { }dS={\displaystyle \iint \limits _{S}} \frac{6x^{2}+6y^{2}+z}{\sqrt{1+4x^{2}+4y^{2}}}dS \]](images/img-1251.png) |
Agora
 |
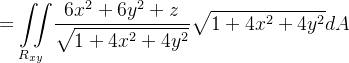 |
|||
 |
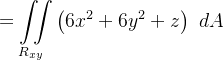 |
da em coordenadas polares
em coordenadas polares
 |
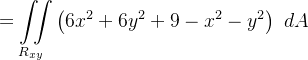 |
|||
 |
 |
|||
 |
 |