| Cálculo Diferencial e Integral 3 |
Considere a figura abaixo, onde  é o gráfico de
é o gráfico de 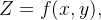 e
e  tem derivadas parciais primeiras cont
tem derivadas parciais primeiras cont nuas e a projeção
nuas e a projeção  de
de  sobre o plano-xy é uma curva que delimita uma região
sobre o plano-xy é uma curva que delimita uma região  da forma considerada no teorema de Green. Nessa figura,
da forma considerada no teorema de Green. Nessa figura,  é uma normal unitária exterior de
é uma normal unitária exterior de  Vamos considerar a direção positiva ao longo de
Vamos considerar a direção positiva ao longo de  como a direção correspondente à direção positiva ao longo de
como a direção correspondente à direção positiva ao longo de  O vetor
O vetor  na figura é um vetor unitário tangente a
na figura é um vetor unitário tangente a  que aponta na direção positiva. Se
que aponta na direção positiva. Se 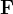 denota um campo vetorial cujas componentes têm derivadas parciais cont
denota um campo vetorial cujas componentes têm derivadas parciais cont nuas numa região contendo
nuas numa região contendo 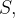 então temos o seguinte resultado, que denominamos o teorema de Stokes.
então temos o seguinte resultado, que denominamos o teorema de Stokes.
Seja 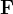 um campo vetorial, cujas componentes têm derivadas parciais cont
um campo vetorial, cujas componentes têm derivadas parciais cont nuas numa região que contém uma superf
nuas numa região que contém uma superf cie
cie 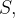 orientável, parametrizada por
orientável, parametrizada por  onde
onde 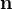 representa o vetor normal unitário exterior de
representa o vetor normal unitário exterior de 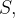 cuja fronteira é dada por uma curva
cuja fronteira é dada por uma curva  no espaço, que tem
no espaço, que tem  como vetor tangente unitário
como vetor tangente unitário então a integral curvil
então a integral curvil nea da componente tangencial de
nea da componente tangencial de 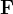 tomada uma vez ao longo da curva
tomada uma vez ao longo da curva  na direção positiva é igual à integral de superf
na direção positiva é igual à integral de superf cie da componente normal de
cie da componente normal de 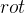
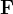 sobre
sobre  Isto é
Isto é
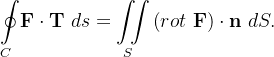 |
(16) |
Seja  a parte do parabolóide
a parte do parabolóide 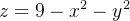 com
com 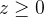 e seja
e seja  o traço de
o traço de  no plano-xy.Verifique o teorema de Stokes
no plano-xy.Verifique o teorema de Stokes 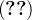 para o campo vetorial
para o campo vetorial 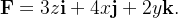
Solução: Devemos mostrar que as duas integrais no teorema  são iguais. Temos que o vetor normal unitário exterior de
são iguais. Temos que o vetor normal unitário exterior de  é:
é:
![\[ \mathbf{n}=\frac{2x\mathbf{i}+2y\mathbf{j}+\mathbf{k}}{\sqrt{4x^{2}+4y^{2}+1}} \]](images/img-1316.png) |
temos o rotacional de 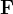 é dado por
é dado por
![\[ rot\ \mathbf{F}\text { }=\left\vert \begin{array}[c]{ccc}\mathbf{i} & \mathbf{j} & \mathbf{k}\\ \frac{\partial }{\partial x} & \frac{\partial }{\partial y} & \frac{\partial }{z}\\ 3z & 4x & 2y \end{array} \right\vert =2\mathbf{i}+3\mathbf{j}+4\mathbf{k} \]](images/img-1317.png) |
Consequentemente,
![\[ {\displaystyle \iint \limits _{S}} \left( rot\ \mathbf{F}\right) \cdot \mathbf{n}\ dS={\displaystyle \iint \limits _{S}} \frac{4x+6y+4}{\sqrt{4x^{2}+4y^{2}+1}}dS \]](images/img-1318.png) |
assim
 |
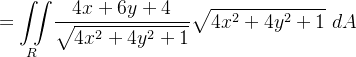 |
|||
 |
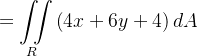 |
onde  é a região do plano-xy delimitada pelo c
é a região do plano-xy delimitada pelo c rculo de raio
rculo de raio 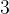 e centro na origem. Passando para coordenadas polares, temos
e centro na origem. Passando para coordenadas polares, temos
 |
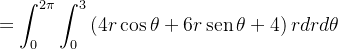 |
|||
 |
![$\displaystyle =\int _{0}^{2\pi }\int _{0}^{3}\left[ \left( 4\cos \theta +6\operatorname {sen}\theta \right) r^{2}+4r\right] drd\theta $](images/img-1324.png) |
|||
 |
![$\displaystyle =\int _{0}^{2\pi }\left[ \left( 4\cos \theta +6\operatorname {sen}\theta \right) \frac{r^{3}}{3}+2r^{2}\right] _{0}^{3}d\theta $](images/img-1325.png) |
|||
 |
 |
|||
 |
![$\displaystyle =\left[ 36\operatorname {sen}\theta -54\cos \theta +18\theta \right] _{0}^{2\pi }=36\pi . $](images/img-1327.png) |
A integral curvil nea do teorema de Stokes pode ser escrita como
nea do teorema de Stokes pode ser escrita como
![\[ {\displaystyle \oint \limits _{C}} \mathbf{F}\cdot \mathbf{T}\ ds={\displaystyle \oint \limits _{C}} \mathbf{F}\cdot d\mathbf{r=}{\displaystyle \oint \limits _{C}} 3zdx+4xdy+2ydz \]](images/img-1328.png) |
onde  é o c
é o c rculo
rculo  no plano-xy. Como
no plano-xy. Como  em
em 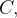 esta integral curvil
esta integral curvil nea se reduz a
nea se reduz a
![\[ {\displaystyle \oint \limits _{C}} \mathbf{F}\cdot d\mathbf{r=}{\displaystyle \oint \limits _{C}} 4xdy=4{\displaystyle \oint \limits _{C}} xdy \]](images/img-1330.png) |
pelo teorema de Green, 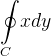 é a área da região (que representa um c
é a área da região (que representa um c rculo de raio
rculo de raio  ) delimitada por
) delimitada por  desse modo,
desse modo,
![\[ {\displaystyle \oint \limits _{C}} \mathbf{F}\cdot d\mathbf{r=}4\left( 9\pi \right) =36\pi . \]](images/img-1332.png) |
Usando o teorema de Stokes podemos obter uma interpretação f sica do rot
sica do rot 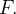 Se
Se 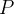 é um ponto arbitrário, seja
é um ponto arbitrário, seja  um disco circular de raio
um disco circular de raio 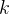 e centro em
e centro em 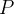 e denotemos por
e denotemos por  a fronteira de
a fronteira de 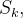 aplicando o teorema de Stokes e um teorema de valor médio para integrais duplas, temos
aplicando o teorema de Stokes e um teorema de valor médio para integrais duplas, temos
![\[ {\displaystyle \oint \limits _{C_{k}}} \mathbf{F}\cdot \mathbf{T}\ ds={\displaystyle \iint \limits _{S_{k}}} \left( rot\ \mathbf{F}\right) \cdot \mathbf{n}\ dS=\left[ rot\ \mathbf{F.n}\right] _{P_{k}}\pi k^{2} \]](images/img-1337.png) |
onde  é um ponto interior de
é um ponto interior de  e
e 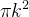 é a área de
é a área de 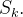 Desse modo,
Desse modo,
![\[ \left[ rot\ \mathbf{F.n}\right] _{P_{k}}=\frac{1}{\pi k^{2}}{\displaystyle \oint \limits _{C_{k}}} \mathbf{F}\cdot \mathbf{T}\ ds \]](images/img-1340.png) |
fazendo  então
então  e assim, obtemos o seguinte resultado.
e assim, obtemos o seguinte resultado.
![\[ \left[ rot\ \mathbf{F.n}\right] _{P}=\lim _{k\rightarrow 0}\frac{1}{\pi k^{2}}{\displaystyle \oint \limits _{C_{k}}} \mathbf{F}\cdot \mathbf{T}\ ds \]](images/img-1343.png) |
Se 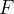 é um campo de velocidade de um fluido, a integral curvilinea
é um campo de velocidade de um fluido, a integral curvilinea 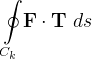 é a circulação em torno de
é a circulação em torno de 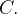 Ela mede a tendência média de fluido se mover, ou circular, ao longo da curva. Vê-se portanto, que
Ela mede a tendência média de fluido se mover, ou circular, ao longo da curva. Vê-se portanto, que ![$\left[ rot\ \mathbf{F.n}\right] $](images/img-1345.png) nos dá informação sobre o movimento de um flu
nos dá informação sobre o movimento de um flu do ao longo da circunferência de um disco circular que é perpendicular a
do ao longo da circunferência de um disco circular que é perpendicular a 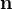 , quando o disco tende a reduzir-se a um ponto. Essa circulação é máxima quando o vetor
, quando o disco tende a reduzir-se a um ponto. Essa circulação é máxima quando o vetor 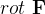 for paralelo ao vetor
for paralelo ao vetor  .
.