| Cálculo Diferencial e Integral 3 |
Seja  uma curva plana suave com parametrização
uma curva plana suave com parametrização
![\[ x=g(t),\ y=h(t),\ \ a\leq t\leq b. \]](images/img-1122.png) |
Suponha que  seja uma curva fechada simples, isto é, existe somente um único ponto de interseção,
seja uma curva fechada simples, isto é, existe somente um único ponto de interseção, 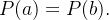 Vamos considerar também que
Vamos considerar também que  está orientada positivamente, isto é, ao longo de
está orientada positivamente, isto é, ao longo de  a região
a região  que
que  encerra estará sempre à esquerda quando o ponto
encerra estará sempre à esquerda quando o ponto 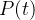 descreve
descreve 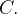 A integral ao longo de uma curva fechada terá a seguinte notação:
A integral ao longo de uma curva fechada terá a seguinte notação:
![\[ {\displaystyle \oint \limits _{C}} M(x,y)dx+N(x,y)dy. \]](images/img-1125.png) |
e chamaremos a integral curvil nea ao longo de uma curva fechada simples
nea ao longo de uma curva fechada simples 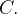 Então temos o seguinte resultado importante que é conhecido como o teorema de Green.
Então temos o seguinte resultado importante que é conhecido como o teorema de Green.
Seja  uma curva fechada simples parcialmente suave e seja
uma curva fechada simples parcialmente suave e seja  a região que consiste de
a região que consiste de  e seu interior. Se
e seu interior. Se 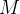 e
e 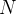 são funções cont
são funções cont nuas com derivadas parciais primeiras cont
nuas com derivadas parciais primeiras cont nuas em toda uma região
nuas em toda uma região 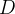 contendo
contendo 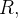 então
então
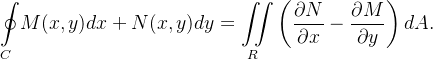 |
(13) |
Consideremos  uma região do tipo
uma região do tipo  ou
ou  isto é,
isto é,
![\[ R=\left\{ \left( x,y\right) :\ a\leq x\leq b,\ g_{1}(x)\leq y\leq g_{2}(x)\right\} =R_{x} \]](images/img-1128.png) |
![\[ R=\left\{ \left( x,y\right) :\ c\leq y\leq d,\ h_{1}(x)\leq y\leq h_{2}(x)\right\} =R_{y} \]](images/img-1129.png) |
onde  e
e  são funções suaves. É suficiente mostrar que
são funções suaves. É suficiente mostrar que
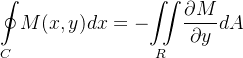 |
(14) |
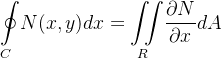 |
(15) |
Prova de 
 consiste de duas curvas suaves
consiste de duas curvas suaves 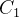 e
e 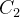 de equações
de equações 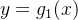 e
e 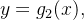 respectivamente. Da
respectivamente. Da
![\[ {\displaystyle \oint \limits _{C}} M(x,y)dx={\displaystyle \oint \limits _{C_{1}}} M(x,y)dx+{\displaystyle \oint \limits _{C_{2}}} M(x,y)dx \]](images/img-1139.png) |
obtemos então que
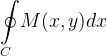 |
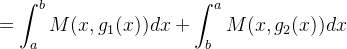 |
|||
 |
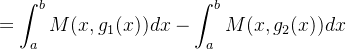 |
Por outro lado,
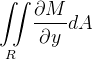 |
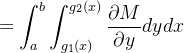 |
|||
 |
![$\displaystyle =\int _{a}^{b}\left[ M(x,y)\right] _{g_{1}(x)}^{g_{2}(x)}dx $](images/img-1145.png) |
|||
 |
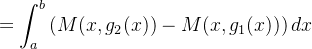 |
segue que:
![\[ {\displaystyle \oint \limits _{C}} M(x,y)dx=-{\displaystyle \iint \limits _{R}} \frac{\partial M}{\partial y}dA \]](images/img-1147.png) |
De modo análogo, considerando  como uma região do tipo
como uma região do tipo 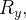 prova-se
prova-se 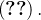 Ou seja,
Ou seja,
![\[ {\displaystyle \oint \limits _{C}} N(x,y)dx={\displaystyle \oint \limits _{C_{1}}} N(x,y)dx+{\displaystyle \oint \limits _{C_{2}}} N(x,y)dx \]](images/img-1149.png) |
obtemos então que
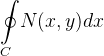 |
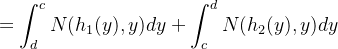 |
|||
 |
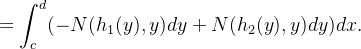 |
Por outro lado,
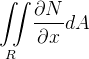 |
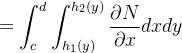 |
|||
 |
![$\displaystyle =\int _{c}^{d}\left[ N(x,y)\right] _{h_{1}(y)}^{h_{2}(y)}dy $](images/img-1155.png) |
|||
 |
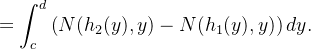 |
o que prova o teorema.
Se 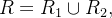
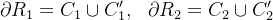 temos
temos
![\[ {\displaystyle \iint \limits _{R_{1}}} \left( \frac{\partial N}{\partial x}-\frac{\partial M}{\partial y}\right) dA={\displaystyle \oint \limits _{C_{1}\cup C_{1}^{\prime }}} Mdx+Ndy \]](images/img-1159.png) |
![\[ {\displaystyle \iint \limits _{R_{2}}} \left( \frac{\partial N}{\partial x}-\frac{\partial M}{\partial y}\right) dA={\displaystyle \oint \limits _{C_{2}\cup C_{2}^{\prime }}} Mdx+Ndy \]](images/img-1160.png) |
A integral ao longo de 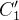 é de sinal contrário à integral ao longo de
é de sinal contrário à integral ao longo de 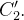 Portanto,
Portanto,
![\[ {\displaystyle \oint \limits _{C}} M(x,y)dx+N(x,y)dy={\displaystyle \iint \limits _{R}} \left( \frac{\partial N}{\partial x}-\frac{\partial M}{\partial y}\right) dA. \]](images/img-1163.png) |
Usando o teorema de Green, calcule 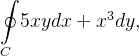 onde
onde  é a curva fechada que consiste nos gráficos de
é a curva fechada que consiste nos gráficos de 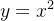 e
e 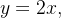 entre os pontos
entre os pontos 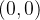 e
e 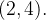
Solução: Pelo teorema de Green: 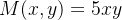 e
e 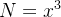 logo
logo
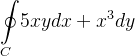 |
![$\displaystyle ={\displaystyle \iint \limits _{R}} \left[ \frac{\partial \left( x^{3}\right) }{\partial x}-\frac{\partial }{\partial y}\left( 5xy\right) \right] dA $](images/img-1170.png) |
|||
 |
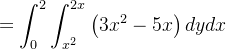 |
|||
 |
![$\displaystyle =\int _{0}^{2}\left[ 3x^{2}y-5xy\right] _{x^{2}}^{2x}dx $](images/img-1172.png) |
|||
 |
![$\displaystyle =\int _{0}^{2}\left[ 11x^{3}-10x^{2}-3x^{4}\right] dx=-\frac{28}{15}. $](images/img-1173.png) |
Usando o teorema de Green, calcule a integral curvil nea
nea
![\[ {\displaystyle \oint \limits _{C}} 2xydx+\left( x^{2}+y^{2}\right) dy \]](images/img-1174.png) |
 é a elipse
é a elipse 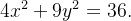
Solução: Pelo teorema de Green, com 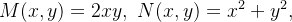 temos
temos
![\[ {\displaystyle \oint \limits _{C}} 2xydx+\left( x^{2}+y^{2}\right) dy={\displaystyle \iint \limits _{R}} (2x-2x)dx={\displaystyle \iint \limits _{R}} 0dA=0. \]](images/img-1177.png) |
A integral sempre será zero para qualquer curva fechada.
Calcule 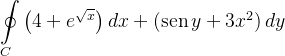 se
se  é a fronteira da região
é a fronteira da região  delimitada pelos quartos de c
delimitada pelos quartos de c rculo de raio
rculo de raio 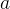 e
e 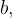 respectivamente, e pelos segmentos de eixo-x e y.
respectivamente, e pelos segmentos de eixo-x e y.
Solução: Por Green
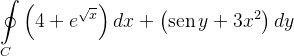 |
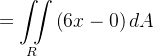 |
|||
 |
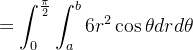 |
|||
 |
![$\displaystyle =6\left[ \frac{1}{3}r^{3}\right] _{a}^{b}\int _{0}^{\frac{\pi }{2}}\cos \theta d\theta $](images/img-1183.png) |
|||
 |
![$\displaystyle =2\left( b^{3}-a^{3}\right) \left[ \operatorname {sen}\theta \right] _{0}^{\frac{\pi }{2}}=2\left( b^{3}-a^{3}\right) . $](images/img-1184.png) |
Usando o teorema de Green podemos encontrar uma fórmula para achar a área  de uma região
de uma região  delimitada por uma curva simples parcialmente suave
delimitada por uma curva simples parcialmente suave 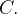 Fazendo
Fazendo 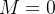 e
e 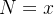 em
em 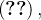 obtemos
obtemos
![\[ A={\displaystyle \iint \limits _{R}} dA={\displaystyle \oint \limits _{C}} xdy \]](images/img-1188.png) |
também se fizermos 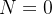 e
e 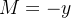 em
em 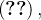 obtemos
obtemos
![\[ A={\displaystyle \iint \limits _{R}} dA=-{\displaystyle \oint \limits _{C}} ydx \]](images/img-1191.png) |
Da , podemos estabelecer o seguinte resultado.
, podemos estabelecer o seguinte resultado.
Se uma região  do plano-xy é delimitada por uma curva fechada, simples, parcialmente suave
do plano-xy é delimitada por uma curva fechada, simples, parcialmente suave 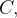 então a área da região
então a área da região 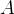 de
de  é
é
![\[ A={\displaystyle \oint \limits _{C}} xdy=-{\displaystyle \oint \limits _{C}} ydx=\frac{1}{2}{\displaystyle \oint \limits _{C}} xdy-ydx. \]](images/img-1192.png) |
Ache a área da elipse usando o teorema de acima.
![\[ \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1. \]](images/img-1193.png) |
Solução: As equações paramétricas da elipse são 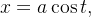
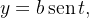
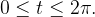 Da
Da
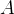 |
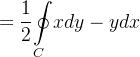 |
|||
 |
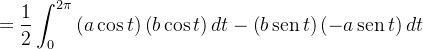 |
|||
 |
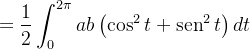 |
|||
 |
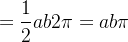 |
O teorema de Green é válido para regiões  que contenha "buracos ". A integração deve ser feita de modo a manter a região
que contenha "buracos ". A integração deve ser feita de modo a manter a região  sempre à esquerda de
sempre à esquerda de  Assim, se tivermos uma região
Assim, se tivermos uma região  cujo contorno exterior seja
cujo contorno exterior seja  e os contornos interiores sejam
e os contornos interiores sejam 
 temos que
temos que
![\[ {\displaystyle \oint \limits _{C_{0}}} M(x,y)dx+N(x,y)dy-\sum _{i=1}^{n}{\displaystyle \oint \limits _{C_{i}}} M(x,y)dx+N(x,y)dy={\displaystyle \iint \limits _{R}} \left( \frac{\partial N}{\partial x}-\frac{\partial M}{\partial y}\right) dA \]](images/img-1204.png) |
onde 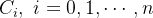 são percorridos no sentido contrário aos ponteiros do relógio.
são percorridos no sentido contrário aos ponteiros do relógio.
Sejam 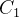 e
e 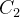 duas curvas fechadas simples parcialmente suaves que não se interceptam, cada uma tendo a origem
duas curvas fechadas simples parcialmente suaves que não se interceptam, cada uma tendo a origem 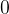 como um ponto interior.Se
como um ponto interior.Se
![\[ M=\frac{-y}{x^{2}+y^{2}},\ \ \ N=\frac{x}{x^{2}+y^{2}} \]](images/img-1206.png) |
prove que
![\[ {\displaystyle \oint \limits _{C_{1}}} M(x,y)dx+N(x,y)dy={\displaystyle \oint \limits _{C_{2}}} M(x,y)dx+N(x,y)dy. \]](images/img-1207.png) |
Solução: Denotando por  a região entre
a região entre 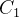 e
e 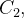 o teorema de Green nos dá
o teorema de Green nos dá
![\[ {\displaystyle \oint \limits _{C_{1}}} M(x,y)dx+N(x,y)dy-{\displaystyle \oint \limits _{C_{2}}} M(x,y)dx+N(x,y)dy={\displaystyle \iint \limits _{R}} \left( \frac{\partial N}{\partial x}-\frac{\partial M}{\partial y}\right) dA \]](images/img-1208.png) |
e como
![\[ \frac{\partial N}{\partial x}=\frac{\left( x^{2}+y^{2}\right) (1)-x\left( 2x\right) }{\left( x^{2}+y^{2}\right) ^{2}}=\frac{y^{2}-x^{2}}{\left( x^{2}+y^{2}\right) ^{2}}=\frac{\partial M}{\partial y} \]](images/img-1209.png) |
a integral dupla sobre  é zero. Consequentemente
é zero. Consequentemente
![\[ {\displaystyle \oint \limits _{C_{1}}} M(x,y)dx+N(x,y)dy={\displaystyle \oint \limits _{C_{2}}} M(x,y)dx+N(x,y)dy. \]](images/img-1207.png) |
Se 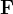 é definida por
é definida por 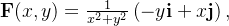 prove que
prove que 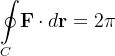 para toda curva fechada simples parcialmente suave que tenha a origem em seu interior.
para toda curva fechada simples parcialmente suave que tenha a origem em seu interior.
Solução: Fazendo 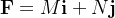 então
então 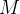 e
e 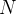 são as mesmas que no exemplo 5. Escolhendo um c
são as mesmas que no exemplo 5. Escolhendo um c rculo
rculo 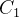 de raio
de raio 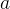 e centro na origem e inteiramente contido em
e centro na origem e inteiramente contido em 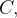 segue que
segue que
![\[ {\displaystyle \oint \limits _{C}} \mathbf{F}\cdot d\mathbf{r=}{\displaystyle \oint \limits _{C_{1}}} \mathbf{F}\cdot d\mathbf{r} \]](images/img-1213.png) |
As equações paramétricas de 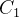 são
são
![\[ x=a\cos t,\ y=a\operatorname {sen}t,\ 0\leq t\leq 2\pi \]](images/img-1214.png) |
obtemos
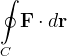 |
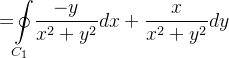 |
|||
 |
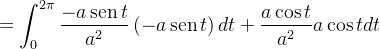 |
|||
 |
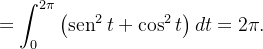 |