11.5 Mudança de representação paramétrica

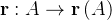Seja $\mathbf{r}:A\rightarrow \mathbf{r}\left( A\right)$ a região do plano- 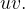$uv.$ Suponha 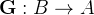$\mathbf{G}:B\rightarrow A$ injetiva e continuamente diferenciável.

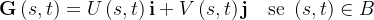$\begin{equation} \mathbf{G}\left( s,t\right) =U\left( s,t\right) \mathbf{i}+V\left( s,t\right) \mathbf{j\ \ \ }\text {se }\left( s,t\right) \in B \label{mudpar1}\end{equation}$

(11)

Considere 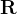$\mathbf{R}$ definida por

$\begin{equation} \mathbf{R}\left( s,t\right) =\mathbf{r}\left[ \mathbf{G}\left( s,t\right) \right] \label{mudpar2}\end{equation}$

(12)

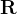$\mathbf{r}$ e $\mathbf{R}$ são regularmente equivalentes, representam a mesma superf $\'{\i }$ cie.

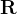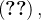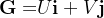Sejam $\mathbf{r}$ e $\mathbf{R}$ regularmente equivalentes ligadas por $\left( \ref{mudpar2}\right) ,$ donde $\mathbf{G=}U\mathbf{i}+V\mathbf{j}$ é injetiva e continuamente diferenciável. Temos então

$\frac{\partial \mathbf{R}}{\partial s}\times \frac{\partial \mathbf{R}}{\partial t}=\left( \frac{\partial \mathbf{r}}{\partial u}\times \frac{\partial \mathbf{r}}{\partial v}\right) \frac{\partial \left( U,V\right) }{\partial \left( s,t\right) }$

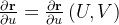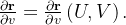
donde $\frac{\partial \mathbf{r}}{\partial u}=\frac{\partial \mathbf{r}}{\partial u}\left( U,V\right)$ e $\frac{\partial \mathbf{r}}{\partial v}=\frac{\partial \mathbf{r}}{\partial v}\left( U,V\right) .$

Demonstração: 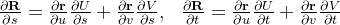$\frac{\partial \mathbf{R}}{\partial s}=\frac{\partial \mathbf{r}}{\partial u}\frac{\partial U}{\partial s}+\frac{\partial \mathbf{r}}{\partial v}\frac{\partial V}{\partial s},\ \ \frac{\partial \mathbf{R}}{\partial t}=\frac{\partial \mathbf{r}}{\partial u}\frac{\partial U}{\partial t}+\frac{\partial \mathbf{r}}{\partial v}\frac{\partial V}{\partial t}$ da $\'{\i }$

$\frac{\partial \mathbf{R}}{\partial s}\times \frac{\partial \mathbf{R}}{\partial t}=\left( \frac{\partial \mathbf{r}}{\partial u}\times \frac{\partial \mathbf{r}}{\partial v}\right) \left( \frac{\partial U}{\partial s}\frac{\partial V}{\partial t}-\frac{\partial U}{\partial t}\frac{\partial V}{\partial s}\right) .$

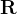Se $\mathbf{r}$ e $\mathbf{R}$ são equivalentes e se 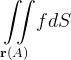${\displaystyle \iint \limits _{\mathbf{r}\left( A\right) }} fdS$ existe então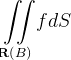 ${\displaystyle \iint \limits _{\mathbf{R}\left( B\right) }} fdS$ $\$ existe e

${\displaystyle \iint \limits _{\mathbf{r}\left( A\right) }} fdS={\displaystyle \iint \limits _{\mathbf{R}\left( B\right) }} fdS.$

Demonstração: 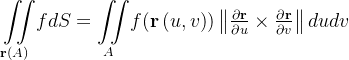${\displaystyle \iint \limits _{\mathbf{r}\left( A\right) }} fdS={\displaystyle \iint \limits _{A}} f(\mathbf{r}\left( u,v\right) )\left\Vert \frac{\partial \mathbf{r}}{\partial u}\times \frac{\partial \mathbf{r}}{\partial v}\right\Vert dudv$ agora

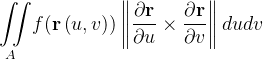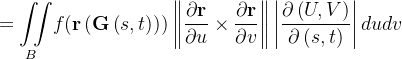	$\displaystyle {\displaystyle \iint \limits _{A}} f(\mathbf{r}\left( u,v\right) )\left\Vert \frac{\partial \mathbf{r}}{\partial u}\times \frac{\partial \mathbf{r}}{\partial v}\right\Vert dudv$	$\displaystyle ={\displaystyle \iint \limits _{B}} f(\mathbf{r}\left( \mathbf{G}\left( s,t\right) \right) )\left\Vert \frac{\partial \mathbf{r}}{\partial u}\times \frac{\partial \mathbf{r}}{\partial v}\right\Vert \left\vert \frac{\partial \left( U,V\right) }{\partial \left( s,t\right) }\right\vert dudv$
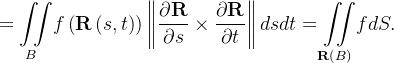	$\displaystyle$	$\displaystyle ={\displaystyle \iint \limits _{B}} f\left( \mathbf{R}\left( s,t\right) \right) \left\Vert \frac{\partial \mathbf{R}}{\partial s}\times \frac{\partial \mathbf{R}}{\partial t}\right\Vert dsdt={\displaystyle \iint \limits _{\mathbf{R}\left( B\right) }} fdS.$