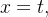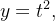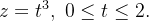| Cálculo Diferencial e Integral 3 |
 cie
cieRepresentação Impl cita:
cita: 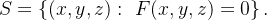 Exemplo:
Exemplo: 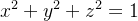 (superf
(superf cie esférica)
cie esférica)
Representação expl cita:
cita: 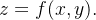 Exemplo:
Exemplo:  e
e 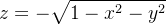 (neste caso, temos a semi-esfera superior e a inferior, respectivamente.)
(neste caso, temos a semi-esfera superior e a inferior, respectivamente.)
Representação Paramétrica: 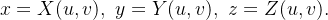
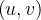 varia num conjunto conexo bidimensional
varia num conjunto conexo bidimensional 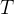 no plano-uv. Os pontos
no plano-uv. Os pontos  correspondem a porções de superf
correspondem a porções de superf cie no espaço-
cie no espaço-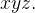
Representação Paramétrica Vetorial:
![\[ \mathbf{r}\left( u,v\right) =X\left( u,v\right) \mathbf{i}+Y\left( u,v\right) \mathbf{j}+Z\left( u,v\right) \mathbf{k,\ }\left( u,v\right) \in T \]](images/img-0965.png) |
![\includegraphics[ trim=0.000000in 0.000000in 0.035984in 0.000000in, height=2.1223in, width=4.6795in ]{Figura7.eps}](images/img-0966.png)
Exemplo 1: Representação paramétrica de uma esfera
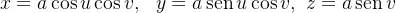 |
(7) |
da obtemos
obtemos
![\[ x^{2}+y^{2}+z^{2}=1 \]](images/img-0968.png) |
se 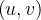 varia no retângulo
varia no retângulo ![$T=\left[ 0,2\pi \right] \times \left[ -\dfrac {\pi }{2},\dfrac {\pi }{2}\right] $](images/img-0969.png) os pontos determinados (7) descrevem toda a esfera. O hemisfério superior é a imagem de um retângulo
os pontos determinados (7) descrevem toda a esfera. O hemisfério superior é a imagem de um retângulo ![$\left[ 0,2\pi \right] \times \left[ 0,\dfrac {\pi }{2}\right] $](images/img-0970.png) e o inferior a imagem de
e o inferior a imagem de ![$\left[ 0,2\pi \right] \times \left[ -\dfrac {\pi }{2},0\right] .$](images/img-0971.png)
![\includegraphics[ height=2.4915in, width=5.7449in ]{Figura9.eps}](images/img-0972.png)
Exemplo 2: Representação vetorial de um cone
![\[ \mathbf{r}\left( u,v\right) =v\operatorname {sen}\alpha \cos u\mathbf{i}+v\operatorname {sen}\alpha \operatorname {sen}u\mathbf{j}+v\cos \alpha \mathbf{k} \]](images/img-0973.png) |
onde 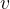 é a distância do vértice ao ponto
é a distância do vértice ao ponto  no cone,
no cone,  é o ângulo polar e
é o ângulo polar e 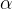
 é ângulo do vértice.
é ângulo do vértice.
![\includegraphics[ height=2.5201in, width=4.1295in ]{Figura10.eps}](images/img-0974.png)
A imagem de 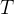 através de
através de  é a superf
é a superf cie paramétrica e representamos por
cie paramétrica e representamos por 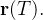 Se a função
Se a função  é injetiva em
é injetiva em 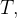 a imagem
a imagem 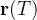 se denominará superf
se denominará superf cie paramétrica simples. Em tal caso, pontos distintos de
cie paramétrica simples. Em tal caso, pontos distintos de 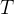 se aplicam em pontos distintos da superf
se aplicam em pontos distintos da superf cie. Em particular, toda curva fechada simples em
cie. Em particular, toda curva fechada simples em 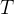 se aplica numa curva fechada simples situada na superf
se aplica numa curva fechada simples situada na superf cie.
cie.
Uma superf cie paramétrica
cie paramétrica  pode degenerar-se num ponto ou em uma curva. Por exemplo,
pode degenerar-se num ponto ou em uma curva. Por exemplo, 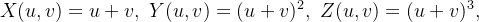 sendo
sendo ![$T=\left[ 0,1\right] \times \left[ 0,1\right] .$](images/img-0979.png) Escrevendo
Escrevendo 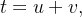 obtemos a curva parametrizada por
obtemos a curva parametrizada por