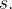| Cálculo Diferencial e Integral 3 |
Seja  uma curva suave dada parametricamente por
uma curva suave dada parametricamente por
![\[ x=f(t),\ y=g(t),\ \ a\leq t\leq b. \]](images/img-0563.png) |
Suponhamos que, além disso, que  não intercepta a si própria, isto é, que valores diferentes de
não intercepta a si própria, isto é, que valores diferentes de  entre
entre 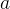 e
e 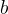 determinam diferentes pontos de
determinam diferentes pontos de  O comprimento de
O comprimento de  de
de 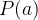 e
e  é dado por
é dado por
![\[ L=\int _{a}^{b}\sqrt{\left( f^{\prime }(t)\right) ^{2}+\left( g^{\prime }(t)\right) ^{2}}dt. \]](images/img-0566.png) |
Seja 


 correspondente a
correspondente a  temos que a distância de
temos que a distância de  a
a  é dada por
é dada por
![\[ d(P_{k-1},P_{k})=\sqrt{\left( f(t_{k})-f(t_{k-1})\right) ^{2}+\left( g(t_{k})-g(t_{k-1})\right) ^{2}}. \]](images/img-0574.png) |
Logo, o comprimento da poligonal que liga os pontos de 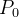 a
a  é
é
![\[ L_{P}=\sum _{k=1}^{n}d(P_{k-1},P_{k}), \]](images/img-0576.png) |
o comprimento da curva será
![\[ L=\lim _{\left\vert P\right\vert \rightarrow 0}L_{P}. \]](images/img-0577.png) |
Usando o teorema do valor médio temos
![\[ \frac{f(t_{k})-f(t_{k-1})}{t_{k}-t_{k-1}}=f^{\prime }(w_{k})\Delta t_{k} \]](images/img-0578.png) |
e
![\[ \frac{g(t_{k})-g(t_{k-1})}{t_{k}-t_{k-1}}=g^{\prime }(w_{k}^{\ast })\Delta t_{k} \]](images/img-0579.png) |
desse modo
![\[ d(P_{k-1},P_{k})=\sqrt{\left( f^{\prime }(w_{k})\right) ^{2}+\left( g^{\prime }(w_{k}^{\ast })\right) }\Delta t_{k} \]](images/img-0580.png) |
e assim
![\[ L=\lim _{\left\vert P\right\vert \rightarrow 0}L_{P}=\lim _{\left\vert P\right\vert \rightarrow 0}\sum _{k=1}^{n}\sqrt{\left( f^{\prime }(w_{k})\right) ^{2}+\left( g^{\prime }(w_{k}^{\ast })\right) }\Delta t_{k} \]](images/img-0581.png) |
logo
![\[ L=\int _{a}^{b}\sqrt{\left( f^{\prime }(t)\right) ^{2}+\left( g^{\prime }(t)\right) }dt. \]](images/img-0582.png) |
Calcule o comprimento de arco da curva C parametrizada por  com
com  .
.
Solucao: O comprimento de arco da curva  é:
é:
![\[ L=\int _{0}^{2}\sqrt{t^{2}+t^{4}}dt=\int _{0}^{2}t\sqrt{1+t^{2}}dt=\frac{1}{2}\int _{1}^{5}\sqrt{u}du=\frac{1}{3}[u^{3/2}]_{1}^{5}=\frac{1}{3}[5^{3/2}-1]. \]](images/img-0585.png) |
Um caminho regular é uma curva  contínua representada por uma função vetorial
contínua representada por uma função vetorial  :
: contínua em
contínua em  e com derivada
e com derivada  contínua em
contínua em  Um caminho é regular por pedaços se ele é a união finita de caminhos regulares.
Um caminho é regular por pedaços se ele é a união finita de caminhos regulares.
Seja  um caminho com derivada
um caminho com derivada  contínua no intervalo
contínua no intervalo ![$J=[a,b].$](images/img-0590.png) A função comprimento de arco
A função comprimento de arco  é dado por
é dado por
![\[ s(t)=\int _{a}^{t}\left\Vert \mathbf{r}^{\prime }(u)\right\Vert du \]](images/img-0592.png) |
A derivada do comprimento de arco é
![\[ s^{\prime }(t)=\left\Vert \mathbf{r}^{\prime }(t)\right\Vert . \]](images/img-0593.png) |
Ou seja, se  :
: é um caminho no plano, por exemplo, então
é um caminho no plano, por exemplo, então
![\[ \mathbf{r}(t)=g(t)i+h(t)j,\ \ a\leq t\leq b,\ \ J=[a,b], \]](images/img-0594.png) |
desse modo,
![\[ s(t)=\int _{a}^{t}\sqrt{\left( g^{\prime }(u)\right) ^{2}+\left( h^{\prime }(u)\right) ^{2}}du \]](images/img-0595.png) |
e
![\[ s^{\prime }(t)=\sqrt{\left( g^{\prime }(t)\right) ^{2}+\left( h^{\prime }(t)\right) ^{2}}. \]](images/img-0596.png) |
Se uma curva  regular, representada pela função vetorial
regular, representada pela função vetorial  e parametrizada pelo comprimento de arco, então o vetor tangente
e parametrizada pelo comprimento de arco, então o vetor tangente  é unitário em cada ponto da curva.
é unitário em cada ponto da curva.
Considere a curva  parametrizada por
parametrizada por
![\[ \overrightarrow {\alpha }=\left\{ \begin{array}[c]{c}x=t\\ y=1-t,\ \ 0\leq t\leq 1 \end{array} \right. \]](images/img-0599.png) |
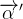 a essa curva, em cada ponto, é unitário.
a essa curva, em cada ponto, é unitário. Solução: Seja
![\[ s=\int _{0}^{t}\sqrt{1+1}dt=\sqrt{2}t \]](images/img-0601.png) |
assim,  Temos então que
Temos então que
![\[ \overrightarrow {\alpha }(s)=\left\{ \begin{array}[c]{c}x=\dfrac {s}{\sqrt{2}}\\ y=1-\dfrac {s}{\sqrt{2}},\ \ 0\leq s\leq \sqrt{2}\end{array} \right. \]](images/img-0603.png) |
Daí
![\[ \overrightarrow {\alpha }^{\prime }(s)=\left\{ \begin{array}[c]{c}x=\dfrac {1}{\sqrt{2}}\\ y=-\dfrac {1}{\sqrt{2}},\ \ 0\leq s\leq \sqrt{2}\end{array} \right. \]](images/img-0604.png) |
e
![\[ \left\Vert \overrightarrow {\alpha }^{\prime }(s)\right\Vert =\sqrt{\frac{1}{2}+\frac{1}{2}}=1. \]](images/img-0605.png) |
A curva  :
: 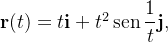

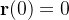 não é regular,
não é regular, 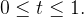
De fato,
![\[ \ \mathbf{r}^{\prime }(t)=\mathbf{i}+\left( 2t\operatorname {sen}\frac{1}{t}-\cos \frac{1}{t}\right) \mathbf{j},\ \ t\neq 0. \]](images/img-0610.png) |
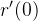 não existe o que implica em
não existe o que implica em 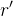 não regular.
não regular.
Uma curva tem infinitas parametrizações e também podemos parametrizar a mesma curva  de modo que a orientação dessa curva mude de sentido. Por exemplo, considere a curva
de modo que a orientação dessa curva mude de sentido. Por exemplo, considere a curva  dada por
dada por
![\[ C:\left\{ \begin{array}[c]{c}x=t\\ y=t^{2},\ \ 0\leq t\leq 2 \end{array} \right. \]](images/img-0613.png) |
e podemos representar a mesma curva por
![\[ -C:\left\{ \begin{array}[c]{c}x=-t\\ y=t^{2},\ \ -2\leq t\leq 0. \end{array} \right. \]](images/img-0614.png) |
Dois caminhos 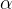 e
e 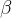 que representam a mesma curva são ditos equivalentes.
que representam a mesma curva são ditos equivalentes.
Tudo que fizemos até agora, pode ser feito para curvas definidas no espaço, por exemplo, se uma curva  :
: 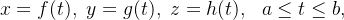 ou podemos considerar a curva representada por uma função vetorial
ou podemos considerar a curva representada por uma função vetorial 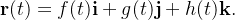 Então o comprimento da curva
Então o comprimento da curva  é dado por
é dado por
![\[ L=\int _{a}^{b}\sqrt{\left( f^{\prime }(t)\right) ^{2}+\left( g^{\prime }(t)\right) ^{2}+(h^{\prime }(t))^{2}}dt \]](images/img-0617.png) |
e a função comprimento de arco é dada por
![\[ s(t)=\int _{a}^{t}\sqrt{\left( f^{\prime }(u)\right) ^{2}+\left( g^{\prime }(u)\right) ^{2}+(h^{\prime }(u))^{2}}du \]](images/img-0618.png) |
e podemos também considerar a curva parametrizada pelo comprimento de arco