7 Derivadas e Integrais de funções vetoriais

Se $\mathbf{r}(t)=\left( f(t),g(t),h(t)\right)$ então

$\lim _{t\rightarrow a}\mathbf{r}(t)=\left( \lim _{t\rightarrow a}f(t),\lim _{t\rightarrow a}g(t),\lim _{t\rightarrow a}h(t)\right)$

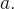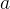desde que $f,g$ e $h$ tenham limites quando $t$ tende a $a.$ Uma função vetorial $\mathbf{r}(t)$ é contínua num ponto $a$ se

$\lim _{t\rightarrow a}\mathbf{r}(t)=\mathbf{r}(a)$

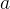segue que $\mathbf{r}(t)=\left( f(t),g(t),h(t)\right)$ é contínua em $a$ se, e somente se, $f,g$ e $h$ o são.

Se $\mathbf{r}(t)$ é uma função vetorial, então a derivada de $\mathbf{r}(t)$ é uma função vetorial $\mathbf{r}^{\prime }(t)$ definida por

$\mathbf{r}^{\prime }(t)=\lim _{\Delta t\rightarrow 0}\frac{1}{\Delta t}\left[ \mathbf{r}(t+\Delta t)-\mathbf{r}(t)\right]$

para todo $t,$ tal que o limite exista.

$\mathbf{r}(t)=f(t)\mathbf{i}+g(t)\mathbf{j}+h(t)\mathbf{k}$

onde $f,$ $g$ e $h$ são funções diferenciáveis, então

$r^{\prime }(t)=f^{\prime }(t)\mathbf{i}+g^{\prime }(t)\mathbf{j}+h^{\prime }(t)\mathbf{k.}$

Considere a função vetorial dada por

$\mathbf{r}(t)=t^{2}\mathbf{i}+\ln (t+1)\mathbf{j}+\operatorname {sen}t\mathbf{k}$

Encontre sua derivada.

Solução:

$r^{\prime }(t)=2t\mathbf{i}+\frac{1}{t+1}\mathbf{j}+\cos t\mathbf{k.}$

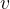Teorema: Sejam $u$ e $v$ duas funções vetoriais e $c\in \mathbb {R}$ então temos o seguinte resultado.

a) 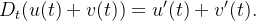$D_{t}(u(t)+v(t))=u^{\prime }(t)+v^{\prime }(t).$

b) 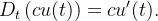$D_{t}\left( cu(t)\right) =cu^{\prime }(t).$

c) $D_{t}\left( u(t)\cdot v(t)\right) =u(t)\cdot v^{\prime }(t)+u^{\prime }(t)\cdot v(t).$

d) $D_{t}(u(t)\times v(t))=u(t)\times v^{\prime }(t)+u^{\prime }(t)\times v(t).$