| Cálculo Diferencial e Integral 3 |
 ndricas e Esféricas
ndricas e EsféricasCoordenadas cil ndricas constituem outra maneira de identificar um ponto no espaço. Dado um ponto
ndricas constituem outra maneira de identificar um ponto no espaço. Dado um ponto 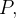 no espaço, sua projeção no eixo-
no espaço, sua projeção no eixo- , fornece a cota
, fornece a cota 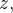 e sua projeção no plano fornece coordenadas polares
e sua projeção no plano fornece coordenadas polares  e
e  As coordenadas cil
As coordenadas cil ndricas de
ndricas de 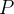 são
são 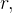
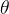 e
e 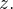 Tomando no plano os eixos-
Tomando no plano os eixos- e
e 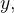 temos as relações
temos as relações 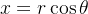 e
e 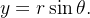 Se
Se 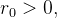 então o gráfico da equação
então o gráfico da equação  ou equivalentemente,
ou equivalentemente, 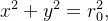 é um cilindro circular reto de raio
é um cilindro circular reto de raio 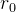 com eixo ao longo do eixo-z.
com eixo ao longo do eixo-z.  Se
Se 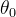 e
e 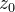 são números reais, então o gráfico de
são números reais, então o gráfico de 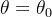 é um plano contendo o eixo-z e o gráfico de
é um plano contendo o eixo-z e o gráfico de 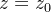 é um plano perpendicular ao eixo-z.
é um plano perpendicular ao eixo-z.
Escreva a equação de  em coordenadas cilindricas e esboce o gráfico.
em coordenadas cilindricas e esboce o gráfico.
Usando coordenadas cilindricas
![\[ z^{2}=r^{2}\text { ou }z=\pm r. \]](images/img-0341.png) |
Escreva a equação em coordenadas retangulares e esboce seu gráfico num sistema de coordenadas xyz.
(a) 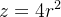 (b)
(b) 
Solução: (a) Temos que
![\[ z=4\left( x^{2}+y^{2}\right) \ \ \text {(parabol\'{o}ide)} \]](images/img-0344.png) |
(b) 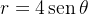 pode ser escrito em coordenadas retangulares da seguinte forma
pode ser escrito em coordenadas retangulares da seguinte forma
![\[ x^{2}+\left( y-2\right) ^{2}=4(cilindrocircularretocentradonoponto\left( 0,2\right) ). \]](images/img-0346.png) |