| Cálculo Diferencial e Integral 2 |
Uma função  de duas variáveis tem máximo local em
de duas variáveis tem máximo local em 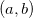 se existe uma vizinhança aberta
se existe uma vizinhança aberta 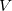 contendo esse ponto tal que
contendo esse ponto tal que 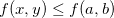 para todo
para todo 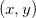 em
em 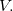 De forma análoga, a função
De forma análoga, a função  tem mínimo local em
tem mínimo local em 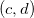 se existe uma vizinhança aberta
se existe uma vizinhança aberta 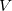 desse ponto tal que
desse ponto tal que 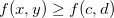 para todo
para todo 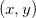 em
em  Se
Se 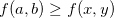 para todo
para todo 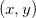 no domínio de
no domínio de  então
então 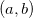 será o ponto de máximo global de
será o ponto de máximo global de  e
e 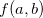 é seu valor máximo, analogamente, se
é seu valor máximo, analogamente, se  para todo
para todo 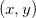 no domínio de
no domínio de  então
então 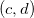 será um ponto de mínimo global de
será um ponto de mínimo global de  e
e 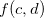 será seu valor mínimo. Os máximos e mínimos locais de uma função
será seu valor mínimo. Os máximos e mínimos locais de uma função  são os extremos locais de
são os extremos locais de 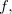 os extremos também incluem os máximos e mínimos globais de
os extremos também incluem os máximos e mínimos globais de  . Uma região
. Uma região  do plano-xy é limitada, se é uma subregião de um disco fechado, isto quer dizer, que existe um número real
do plano-xy é limitada, se é uma subregião de um disco fechado, isto quer dizer, que existe um número real 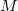 positivo, tal que
positivo, tal que
![\[ |x|\leq M, \forall \, x \in R \]](images/img-0803.png) |
Se  é contínua numa região fechada e limitada
é contínua numa região fechada e limitada  então
então  tem máximo e mínimo em
tem máximo e mínimo em  , isto é, existem pontos
, isto é, existem pontos 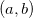 e
e 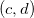 em
em  tais que
tais que
![\[ f(c,d)\leq f(x,y)\leq f(a,b) \quad \forall \, (x,y)\in R. \]](images/img-0804.png) |
Se  tem derivadas parciais primeiras contínuas em
tem derivadas parciais primeiras contínuas em 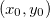 e se
e se 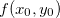 é um extremo local de
é um extremo local de  , então o plano tangente ao gráfico de
, então o plano tangente ao gráfico de 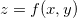 em
em 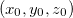 é paralelo ao plano-xy e, assim, sua equação é
é paralelo ao plano-xy e, assim, sua equação é 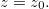 Segue que
Segue que 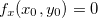 e
e 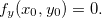
Definição 14. Seja  uma função de duas variáveis. Um par
uma função de duas variáveis. Um par 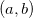 é ponto crítico de
é ponto crítico de  se
se
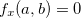 e
e 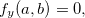 ou,
ou, 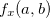 ou
ou 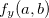 não existe.
não existe.
Um máximo ou mínimo de uma função  , podem ocorrer num ponto fronteira de seu domínio
, podem ocorrer num ponto fronteira de seu domínio  .
.
Exemplo 48. Seja 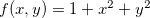 , com
, com  . Ache os extremos de
. Ache os extremos de  .
.
Solução: Por definição os pontos críticos de  são soluções do seguinte sistema
são soluções do seguinte sistema
![\[ \begin{cases} f_ x(x,y)=0 \\ f_ y(x,y)=0 \end{cases} \quad \text {ou}\quad \begin{cases} 2x=0 \\ 2y=0 \end{cases} \]](images/img-0815.png) |
que tem como solução 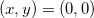 , logo,
, logo, 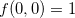 é o único extremo da função
é o único extremo da função  e notamos que esse valor é o valor mínimo dessa função e, portanto,
e notamos que esse valor é o valor mínimo dessa função e, portanto, 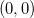 é o ponto de mínimo local de
é o ponto de mínimo local de  , que é também o mínimo global de
, que é também o mínimo global de  , já que,
, já que,  se
se 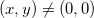 . Para achar possíveis extremos na fronteira, investigamos pontos
. Para achar possíveis extremos na fronteira, investigamos pontos 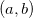 que estejam na fronteira de
que estejam na fronteira de  . Um desses pontos é o
. Um desses pontos é o  que conduz a
que conduz a  . Que é o valor máximo, pois,
. Que é o valor máximo, pois,
![\[ 1+x^2+y^2\leq 1+4=5, \]](images/img-0822.png) |
para todo 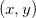 tal que
tal que  . Assim, todos os pontos de fronteira de
. Assim, todos os pontos de fronteira de  serão pontos de màximo de
serão pontos de màximo de  .
.
Exemplo 49. Se 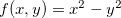 e o domínio de
e o domínio de  é o
é o 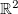 , ache os extremos de
, ache os extremos de  .
.
Solução: Por definição, os pontos críticos são soluções do seguinte sistema:
![\[ \begin{cases} f_ x(x,y)=0 \\ f_ y(x,y)=0 \end{cases} \quad \text {ou}\quad \begin{cases} 2x=0 \\ -2y=0 \end{cases} \]](images/img-0824.png) |
o único extremo local possível é o 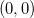 . Mas se
. Mas se 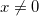 , então
, então 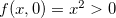 , e se
, e se 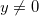 , então
, então 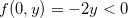 . Qualquer disco aberto no plano-xy que contenha o
. Qualquer disco aberto no plano-xy que contenha o 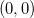 contém pares nos quais os valores funcionais são maiores do
contém pares nos quais os valores funcionais são maiores do 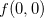 e também pares em que os valores de
e também pares em que os valores de  são menores que
são menores que  Logo,
Logo,  não possui ponto de máximo nem ponto de mínimo e o ponto
não possui ponto de máximo nem ponto de mínimo e o ponto 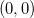 é chamado ponto de sela.
é chamado ponto de sela.
Definição 15. Seja  uma função de duas variáveis com derivadas parciais segundas contínuas, ou seja,
uma função de duas variáveis com derivadas parciais segundas contínuas, ou seja, 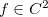 . O discriminante
. O discriminante 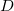 de
de  é
é
![\[ D(x,y)=f_{xx}(x,y)f_{yy}(x,y)-[f_{xy}(x,y)]^2. \]](images/img-0831.png)
Teorema 22 (Teste para extremos locais). Seja máximo local de mínimo local de  uma função de duas variáveis com derivadas parciais segundas contínuas no disco aberto
uma função de duas variáveis com derivadas parciais segundas contínuas no disco aberto  que contém
que contém 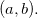 Se
Se 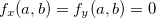 e
e 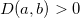 , então
, então 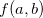 é
é
 se
se 
 se
se 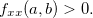
Note que 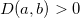 implica em
implica em ![$f_{xx}(a,b)f_{yy}(a,b)>[f_{xy}(a,b)]^2$](images/img-0836.png) o que implica em
o que implica em 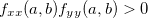 , logo, se
, logo, se 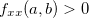 devemos ter também que
devemos ter também que 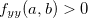 e que se
e que se  então
então 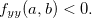
Exemplo 50. Seja 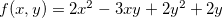 . Ache os pontos de extremos de
. Ache os pontos de extremos de  .
.
Solução: Temos que
![\[ f_ x=4x-3y \quad \text {e}\quad f_ y=-3x+4y+2 \]](images/img-0843.png) |
assim temos o sistema
![\[ \begin{cases} 4x-3y=0\\ -3x+4y+2=0 \end{cases} \]](images/img-0844.png) |
então o único ponto crítico dessa função é 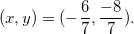 Agora temos que
Agora temos que
![\[ f_{xx}(-6/7,-8/7)=4, \quad f_{yy}=4, \quad f_{xy}=-3 \]](images/img-0846.png) |
logo,
![\[ D(x,y)=4.4-(-3)^2=16-9=7>0 \]](images/img-0847.png) |
e como 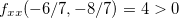 então o ponto
então o ponto 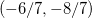 é ponto de mínimo local de
é ponto de mínimo local de  .
.
Exemplo 51. Ache os extremos da função 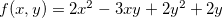 na região retangular
na região retangular 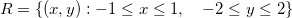 .
.
Solução: Note que o ponto 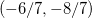 pertence a essa região retangular, e como vimos no exemplo 50 esse ponto é o único ponto crítico dessa função, portanto, dentro dessa região só temos um ponto de mínimo local que é o ponto
pertence a essa região retangular, e como vimos no exemplo 50 esse ponto é o único ponto crítico dessa função, portanto, dentro dessa região só temos um ponto de mínimo local que é o ponto 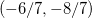 . Analisemos agora os pontos de fronteira de
. Analisemos agora os pontos de fronteira de  , a fronteira de
, a fronteira de  consiste de quatro segmentos retilíneos,
consiste de quatro segmentos retilíneos,  ,
,  ,
, 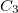 e
e 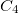 que formam o retângulo. Seja
que formam o retângulo. Seja 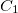 o segmento correspondente a
o segmento correspondente a 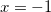 e
e 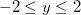 , temos, para esse segmento, que
, temos, para esse segmento, que 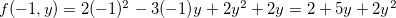 . Assim obtemos a função
. Assim obtemos a função  definida para
definida para 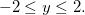 Procurando um ponto crítico para
Procurando um ponto crítico para 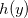 temos
temos  o que implica em
o que implica em 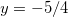 e, como,
e, como, 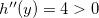 então esse ponto é ponto de mínimo local no intervalo
então esse ponto é ponto de mínimo local no intervalo 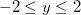 assim, o ponto
assim, o ponto 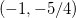 é, a priori, um ponto de mínimo local em
é, a priori, um ponto de mínimo local em  . Escolhamos agora o segmento
. Escolhamos agora o segmento 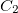 correspondente a
correspondente a 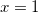 e
e 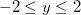 obtemos
obtemos 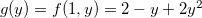 , procurando um ponto crítico de
, procurando um ponto crítico de 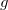 temos
temos  , assim,
, assim, 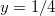 e
e  , assim o ponto
, assim o ponto 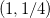 é, a priori, ponto de mínimo local de
é, a priori, ponto de mínimo local de  . Consideremos agora o segmento
. Consideremos agora o segmento 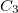 correspondente a
correspondente a 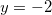 e
e 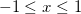 temos
temos 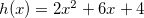 , desse modo, temos que
, desse modo, temos que 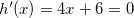 obtemos o ponto
obtemos o ponto 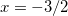 que está fora do intervalo
que está fora do intervalo 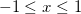 , o que significa que estamos fora da região
, o que significa que estamos fora da região  . Finalmente, considerando o segmento
. Finalmente, considerando o segmento 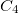 correspondente a
correspondente a 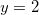 e
e 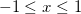 temos
temos 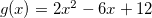 e daí,
e daí, 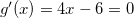 o que implica em
o que implica em 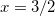 que está fora de
que está fora de  . Agora vamos considerar uma tabela com todos os pontos encontrados e seus respectivos valores de
. Agora vamos considerar uma tabela com todos os pontos encontrados e seus respectivos valores de  incluindo os quatro pontos que são os vértices da região
incluindo os quatro pontos que são os vértices da região  .
.
Pontos |
Valor de |
Pontos Extremos |
|
Ponto interior de |
|
|
Mínimo local (global) |
Ponto no segmento |
|
|
Mínimo local em |
Ponto no segmento |
|
|
Mínimo local em |
Vértice 1 |
|
|
|
Vértice 2 |
|
|
Máximo global |
Vértice 3 |
|
|
|
Vértice 4 |
|
|

Um ponto  é um ponto de sela de uma função
é um ponto de sela de uma função  se
se 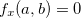 ,
, 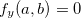 e, se existe uma bola
e, se existe uma bola 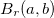 , tal que
, tal que 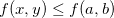 para algum ponto
para algum ponto  e
e 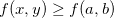 para algum ponto
para algum ponto  .
.
Teorema 23. Seja 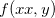 uma função de classe
uma função de classe 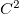 num disco aberto
num disco aberto 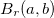 . Se
. Se 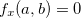 ,
, 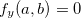 e
e  então o ponto
então o ponto  é ponto de sela do gráfico de
é ponto de sela do gráfico de  .
.
Exemplo 52. Se  , ache os extremos locais e os pontos de sela de
, ache os extremos locais e os pontos de sela de  , se existirem.
, se existirem.
Solução: As derivadas parciais primeiras de  são
são
![\[ f_ x=2x-2y, \quad f_ y=-2x+3y^2-1 \]](images/img-0900.png) |
daí, temos que o sistema
![\[ \begin{cases} 2x-2y=0\\ -2x+3y^2-1=0 \end{cases} \]](images/img-0901.png) |
o que implica que os pontos críticos de  são:
são:
![\[ (1,1) \quad (-1/3,-1/3) \]](images/img-0902.png) |
temos que
![\[ f_{xx}(x,y)=2, \quad f_{yy}(x,y)=6y, \quad f_{xy}=-2 \]](images/img-0903.png) |
assim
![\[ D(x,y)=12y-4 \]](images/img-0904.png) |
então temos a tabela
Pontos críticos |
Discriminante |
Valor de |
Conclusão |
(1,1) |
|
|
|
|
|
irrel |
|
