| Cálculo Diferencial e Integral 2 |
Suponhamos que uma superfície  seja o gráfico da equação
seja o gráfico da equação 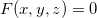 e que
e que 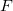 tenha derivadas parciais primeiras contínuas. Seja
tenha derivadas parciais primeiras contínuas. Seja 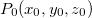 um ponto de
um ponto de  no qual
no qual 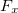 ,
, 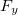 e
e 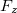 não sejam simultaneamente nulos. uma reta tangente a
não sejam simultaneamente nulos. uma reta tangente a  em
em 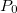 é, por definição, uma reta
é, por definição, uma reta 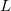 tangente a qualquer curva
tangente a qualquer curva 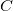 de
de  que contenha
que contenha 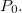 Se
Se 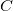 admite a parametrização
admite a parametrização
![\[ x=f(t), \quad y=g(t),\quad z=h(t) \]](images/img-0709.png) |
para 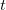 em algum intervalo
em algum intervalo 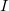 e se
e se 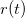 é o vetor posição de
é o vetor posição de 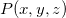 , então
, então
![\[ r(t)=f(t)\vec{i}+g(t)\vec{j}+h(t)\vec{k}. \]](images/img-0711.png) |
Logo,
![\[ r’(t)=f’(t)\vec{i}+g’(t)\vec{j}+h’(t)\vec{k} \]](images/img-0712.png) |
é um vetor tangente a 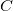 em
em 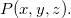 Para cada
Para cada  o ponto
o ponto 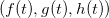 de
de  também pertence a
também pertence a  e, portanto,
e, portanto,
![\[ F(f(t),g(t),h(t))=0. \]](images/img-0715.png) |
Fazendo
![\[ W=F(x,y,z) \]](images/img-0716.png) |
com 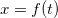 ,
, 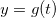 , e
, e 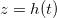 , então, pela regra da cadeia, e como
, então, pela regra da cadeia, e como 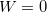 para todo
para todo 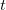 , temos
, temos
![\[ \dfrac {dW}{dt}=\dfrac {\partial W}{\partial x}\dfrac {dx}{dt}+\dfrac {\partial W}{\partial y}\dfrac {dy}{dt}+\dfrac {\partial W}{\partial z}\dfrac {dz}{dt}=0; \]](images/img-0721.png) |
Assim, para todo ponto 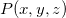 de
de 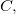
![\[ F_ x(x,y,z)f’(t)+F_ y(x,y,z)g’(t)+F_ z (x,y,z)h’(t)=0, \]](images/img-0723.png) |
ou equivalentemente
![\[ \nabla F(x,y,z) \cdot r’(t)=0. \]](images/img-0724.png) |
Em particular, se 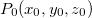 corresponde a
corresponde a 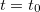 então
então
![\[ \nabla F|_{P_0} \cdot r’(t_0)=\nabla F(x_0,y_0,z_0) \cdot r’(t_0)=0 \]](images/img-0726.png) |
Como 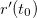 é um vetor tangente a
é um vetor tangente a 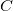 em
em 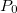 , isto implica que o vetor
, isto implica que o vetor 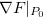 é ortogonal a toda reta tangente
é ortogonal a toda reta tangente 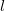 a
a  em
em 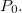 O plano que passa por
O plano que passa por 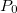 com vetor normal
com vetor normal 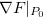 é o plano tangente a
é o plano tangente a  em
em 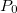 . (Mostramos que toda reta tangente
. (Mostramos que toda reta tangente 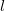 a
a  em
em 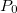 está no plano tangente em
está no plano tangente em 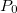 .)
.)
Teorema 19. Seja 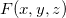 uma função de três variáveis com derivadas parciais primeiras contínuas, e seja
uma função de três variáveis com derivadas parciais primeiras contínuas, e seja  o gráfico de
o gráfico de 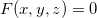 em
em 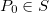 , com
, com 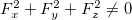 em
em 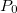 então
então 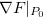 é normal ao plano tangente a
é normal ao plano tangente a  em
em 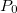 .
.
O vetor 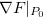 do teorema 19 é designado como a normal à superfície
do teorema 19 é designado como a normal à superfície  em
em 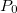 .
.
Corolário 4. A equação do plano tangente ao gráfico de 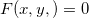 no ponto
no ponto 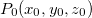 é
é
![\[ F_ x(x_0,y_0,z_0)(x-x_0)+F_ y(x_0,y_0,z_0)(y-y_0)+F_ z(x_0,y_0,z_0)(z-z_0)=0. \]](images/img-0735.png)
Podemos também descrever o plano tangente como
![\[ \nabla F(x_0,y_0,z_0)\cdot [(x-x_0)\vec{i}+(y-y_0)\vec{j}+(z-z_0)\vec{k}]=0 \]](images/img-0736.png) |
Exemplo 44. Ache a equação do plano tangente ao elipsóide 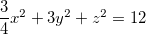 no ponto
no ponto 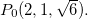
Solução: Para usar o corolário 4 expressamos inicialmente, a equação de superfície na forma 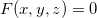 onde
onde
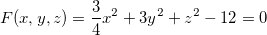 |
(3.1) |
As derivadas parciais de 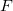 são
são
![\[ F_ x=\dfrac {3}{2}x, \quad F_ y=6y, \quad F_ z=2z \]](images/img-0740.png) |
e, então em 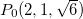 temos
temos
![\[ F_ x(2,1,\sqrt{6})=3, \quad F_ y(2,1,\sqrt{6})=6, \quad F_ z(2,1,\sqrt{6})=2\sqrt{6} \]](images/img-0742.png) |
aplicamos o corolário, obtendo
![\[ 3(x-2)+6(y-1)+2\sqrt{6}(z-\sqrt{6})=0 \]](images/img-0743.png) |
ou
![\[ 3x+6y+2\sqrt{6}z=24 \]](images/img-0744.png) |
e o vetor normal à superfície  dada pela equação (3.1) é o vetor
dada pela equação (3.1) é o vetor
![\[ \nabla F|_{P_0}=\nabla F(2,1,\sqrt{6})=3\vec{i}+6\vec{j}+2\sqrt{6}\vec{k} \]](images/img-0745.png) |
Se 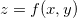 é a equação de
é a equação de  , e fazendo
, e fazendo 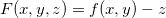 , então a equação do corolário 4 toma a forma
, então a equação do corolário 4 toma a forma
![\[ f_ x(x_0,y_0)(x-x_0)+f_ y(x_0,y_0)(y-y_0)+ (-1)(z-z_0)=0 \]](images/img-0747.png) |
onde 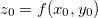 .
.
Teorema 20. A equação do plano tangente ao gráfico de 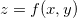 no ponto
no ponto 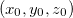 é
é
![\[ z-z_0=f_ x(x_0,y_0)(x-x_0)+f_ y(x_0,y_0)(y-y_0) \]](images/img-0750.png)
A reta perpendicular ao plano tangente no ponto 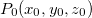 de uma superfície
de uma superfície  é a reta normal a
é a reta normal a  em
em 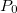 .Se
.Se  é o gráfico de
é o gráfico de 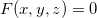 , então a normal é paralela ao vetor
, então a normal é paralela ao vetor 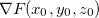 .
.
Exemplo 45. Ache a equação da reta normal ao elipsóide 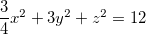 no ponto
no ponto 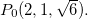
Solução: Temos que
![\[ \nabla F|_{P_0}=\nabla F(2,1,\sqrt{6})=3\vec{i}+6\vec{j}+2\sqrt{6}\vec{k} \]](images/img-0752.png) |
daí, a reta normal ao elipsóide é
![\[ x=2+3t, \quad y=1+6t, \quad z=\sqrt{6}+2\sqrt{6}t, \]](images/img-0753.png) |
com  variando em
variando em 
Seja  o gráfico da equação
o gráfico da equação  O plano tangente a
O plano tangente a  no ponto
no ponto 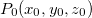 permite obter uma interpretação geométrica para a diferencial:
permite obter uma interpretação geométrica para a diferencial:
![\[ dz=f_ x(x_0,y_0)\Delta x+f_ y(x_0,y_0)\Delta y. \]](images/img-0755.png) |
Como
![\[ \Delta z=f(x_0+\Delta x, y_0+\Delta y)-f(x_0,y_0) \]](images/img-0756.png) |
o ponto 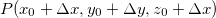 está em
está em 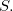
Seja 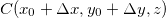 um ponto no plano tangente, e consideremos os pontos
um ponto no plano tangente, e consideremos os pontos 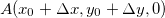 e
e 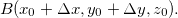 Como
Como 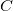 está no plano tangente suas coordenadas vericam a equação do plano tangente, isto é,
está no plano tangente suas coordenadas vericam a equação do plano tangente, isto é,
![\[ z-z_0=f_ x(x_0,y_0)(x_0+\Delta -x_0) x+f_ y(x_0,y_0)(y_0+\Delta y-y_0) \]](images/img-0762.png) |
![\[ =f_ x(x_0,y_0)\Delta x+f_ y(x_0,y_0)\Delta y=dz \]](images/img-0763.png) |
0u seja, 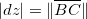 ,
, 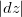 é a distância de
é a distância de  ao ponto do plano tangente, diretamente acima (ou abaixo) de
ao ponto do plano tangente, diretamente acima (ou abaixo) de 
Suponha que temos uma função  de três variáveis dada por
de três variáveis dada por
![\[ w=F(x,y,z) \]](images/img-0768.png) |
se o ponto 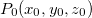 é um ponto fixo, então o gráfico da equação:
é um ponto fixo, então o gráfico da equação:
![\[ F(x,y,z)=f(x_0,y_0,z_0) \]](images/img-0769.png) |
é a superfície de nível que passa pelo ponto 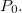 Em todo ponto dessa superfície o valor de
Em todo ponto dessa superfície o valor de  é sempre o mesmo
é sempre o mesmo 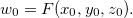 Pelo teorema 19,
Pelo teorema 19, 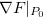 ,
, 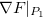 e
e 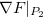 são vetores normais às suas superfícies correspondentes nos pontos
são vetores normais às suas superfícies correspondentes nos pontos 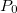 ,
, 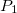 e
e 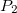 , respectivamente.
, respectivamente.
Vimos que a taxa máxima de variação de 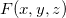 em
em 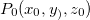 ocorre na direção do gradiente de
ocorre na direção do gradiente de 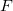 , nesse ponto, isto é na direção de
, nesse ponto, isto é na direção de 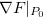 . Pelo que vimos, esta taxa máxima de variação ocorre na direção que é normal à superfície de nível de
. Pelo que vimos, esta taxa máxima de variação ocorre na direção que é normal à superfície de nível de 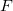 que contém
que contém 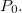
Teorema 21. Seja 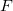 uma função de três variáveis diferenciável em
uma função de três variáveis diferenciável em 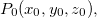 e
e  a superfície de nível de
a superfície de nível de  que contém
que contém 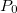 . Se
. Se 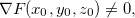 então este vetor gradiente é normal a
então este vetor gradiente é normal a  em
em 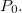 Assim a direção da taxa máxima de variação de
Assim a direção da taxa máxima de variação de 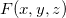 em
em 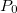 é normal a
é normal a 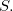
Exemplo 46. Se 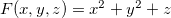 esboce a superfície de nível de
esboce a superfície de nível de 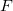 que passa pelo ponto
que passa pelo ponto 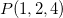 , diga quem é
, diga quem é 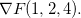
Solução: As superfícies de nível de 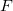 são gráficos de equações da forma
são gráficos de equações da forma
![\[ F(x,y,z)=k, \quad k \quad \text {constante} \]](images/img-0781.png) |
Como 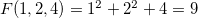 a superfície de nível que passa por
a superfície de nível que passa por 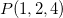 é o gráfico da equação
é o gráfico da equação 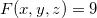 , isto é,
, isto é,
![\[ z=9-x^2-y^2. \]](images/img-0784.png) |
Esta superfície é o parabolóide circular com concavidade para baixo e com vértice no ponto 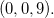
O gradiente de 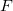 é:
é:
![\[ \nabla F=2x \vec{i}+ 2y\vec{j}+\vec{k} \]](images/img-0786.png) |
e em 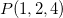 temos que
temos que
![\[ \nabla F(1,2,4)=2(1)\vec{i}+2(2)\vec{j}+\vec{k}=2\vec{i}+4\vec{j}+\vec{k}. \]](images/img-0787.png) |
Exemplo 47. Seja Trace a curva de nível Discuta o significado de (1) em torno do gráfico de 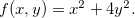
 de
de  que passa pelo ponto
que passa pelo ponto 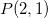 e esboce
e esboce 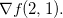
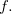
Solução:
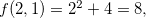 assim
assim 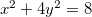 (elipse) e
(elipse) e 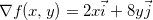 o que implica em
o que implica em 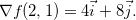
O gráfico de 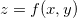 é um parabolóide elíptico, a equação
é um parabolóide elíptico, a equação 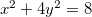 é a curva de nível de
é a curva de nível de  correspondente a
correspondente a 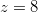 e o
e o 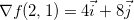 é a direção da taxa máxima de variação de
é a direção da taxa máxima de variação de  no ponto
no ponto 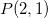 .
.