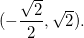| Cálculo Diferencial e Integral 2 |
Em muitas aplicações devemos achar os extremos de uma função  sujeita a algum vínculo. Por exemplo, encontrar o volume da maior caixa retangular cujas faces sejam paralelas aos planos coordenados que esteja inserida no elipsóide de equação,
sujeita a algum vínculo. Por exemplo, encontrar o volume da maior caixa retangular cujas faces sejam paralelas aos planos coordenados que esteja inserida no elipsóide de equação, 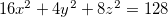 , temos que
, temos que  onde
onde 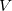 representa o volume da caixa, daí
representa o volume da caixa, daí 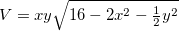 . Temos então o seguinte teorema devido a Lagrange.
. Temos então o seguinte teorema devido a Lagrange.
Teorema 24. Sejam  e
e 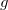 funções de duas variáveis de classe
funções de duas variáveis de classe 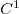 , e suponhamos que
, e suponhamos que 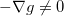 numa região do plano-xy. Se
numa região do plano-xy. Se  tem um extremo
tem um extremo 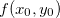 sujeito ao vínculo
sujeito ao vínculo 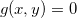 então existe um número real
então existe um número real 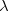 tal que
tal que
![\[ \nabla f(x_0,y_0)=\lambda \nabla g(x_0,y_0). \]](images/img-0918.png)
Prova: O gráfico de 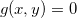 é uma curva
é uma curva 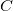 no plano-xy. Suponha que
no plano-xy. Suponha que 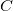 admite a parametrização:
admite a parametrização:
![\[ x=h(t), \quad y=k(t), \quad t \in I. \]](images/img-0919.png) |
Seja
![\[ \vec{r}(t)=x\vec{i}+y\vec{j}=h(t)\vec{i}+k(t)\vec{j}, \]](images/img-0920.png) |
suponha que  tem um extremo em
tem um extremo em 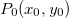 tal que
tal que 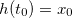 e
e 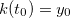 . Definindo uma função
. Definindo uma função 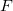 de uma variável por
de uma variável por
![\[ F(t)=f(h(t),k(t)) \]](images/img-0923.png) |
quando 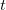 varia obtemos
varia obtemos  com
com 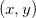 variando em
variando em 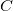 , isto é,
, isto é,  está sujeita ao vínculo
está sujeita ao vínculo 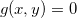 . Como
. Como 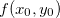 é um valor extremo de
é um valor extremo de  , sob estas condições, segue que
, sob estas condições, segue que 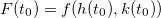 é um extremo de
é um extremo de 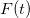 . Assim,
. Assim, 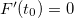 .
.  como função composta pode ser derivada de modo que
como função composta pode ser derivada de modo que
![\[ F’(t)=\dfrac {\partial f}{\partial x}\dfrac {dx}{dt}+\dfrac {\partial f}{\partial y}\dfrac {dy}{dt} \]](images/img-0927.png) |
![\[ F’(t)=\dfrac {\partial f}{\partial x}h’(t)+\dfrac {\partial f}{\partial y}k’(t) \]](images/img-0928.png) |
Fazendo 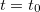 temos
temos
![\[ 0=F’(t_0)=\dfrac {\partial f}{\partial x}(x_0,y_0)h’(t_0)+\dfrac {\partial f}{\partial y}(x_0,y_0)k’(t_0)=\nabla f(x_0,y_0)\cdot \vec{r}’(t_0) \]](images/img-0929.png) |
Isto mostra que o vetor 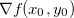 é ortogonal ao vetor
é ortogonal ao vetor 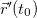 tangente a
tangente a 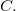 Mas
Mas 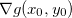 também é ortogonal a
também é ortogonal a 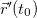 , pois
, pois 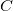 é uma curva de nível para
é uma curva de nível para 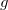 . Como
. Como 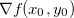 e
e 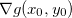 são ortogonais ao mesmo vetor, então eles são paralelos, isto é, existe um
são ortogonais ao mesmo vetor, então eles são paralelos, isto é, existe um 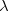 real tal que
real tal que
![\[ \nabla f(x_0,y_0)=\lambda \nabla g(x_0,y_0) \]](images/img-0934.png) |
o número 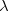 é o multiplicador de Lagrange.
é o multiplicador de Lagrange.
O teorema de Lagrange 24 nos diz que os pontos extremos de uma função  sujeita ao vínculo
sujeita ao vínculo 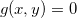 serão os pontos
serão os pontos 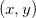 determinados pelas duas primeiras coordenadas de
determinados pelas duas primeiras coordenadas de 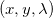 que são soluções do sistema
que são soluções do sistema
![\[ \begin{cases} f_ x(x,y)=\lambda g_ x (x,y)\\ f_ y(x,y)=\lambda g_ y (x,y)\\ g(x,y)=0 \end{cases} \]](images/img-0936.png) |
Exemplo 53. Ache os extremos de 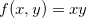 se
se 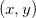 está restrito à elipse
está restrito à elipse 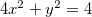 .
.
Solução: Temos que 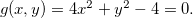 Fazendo
Fazendo 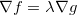 obtemos
obtemos
![\[ y\vec{i}+x\vec{j}=\lambda (8x\vec{i}+2y\vec{j}) \]](images/img-0941.png) |
Assim obtemos o seguinte sistema:
![\[ \begin{cases} y=\lambda 8 x\\ x=\lambda 2y\\ 4x^2+y^2-4=0 \end{cases} \]](images/img-0942.png) |
fazendo 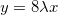 em
em 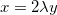 obtemos
obtemos
![\[ x=2\lambda (8\lambda x)=16 \lambda ^2 x \]](images/img-0945.png) |
ou
![\[ (1-16\lambda ^2)x=0. \]](images/img-0946.png) |
Portanto, ou 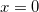 ou
ou 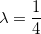 se
se 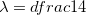 obtemos
obtemos
![\[ y=8\lambda x=8x(\dfrac {1}{4})=2x. \]](images/img-0950.png) |
Levando em conta este valor teremos
![\[ 4x^2+4x-4=0, \Rightarrow 8x^2=4 \]](images/img-0951.png) |
ou
![\[ x=\dfrac {1}{\sqrt{2}}=\dfrac {\sqrt{2}}{2} \]](images/img-0952.png) |
os valores correspondentes de  são
são
![\[ y=2x=2\dfrac {\sqrt{2}}{2}=\sqrt{2} \]](images/img-0953.png) |
assim obtemos os pontos 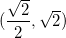 e
e 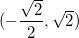 temos a seguinte tabela
temos a seguinte tabela
desse modo,  toma valor máximo
toma valor máximo  em
em 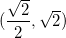 ou
ou 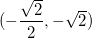 e valor mínimo
e valor mínimo 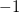 em
em 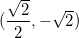 ou
ou