3.1 Derivada Direcional
Seja 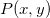 um ponto do plano e
um ponto do plano e 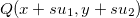 onde
onde 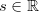 , temos então que o vetor
, temos então que o vetor 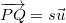 onde
onde 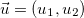 e consideramos
e consideramos 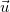 como um vetor unitário. Então
como um vetor unitário. Então
Se a posição de um ponto  varia de
varia de  para
para 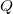 então o incremento
então o incremento 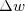 de
de 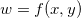 é
é
A taxa média de variação de  é
é
Definição 12. Sejam 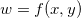 e
e 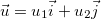 um vetor unitário. A derivada direcional de
um vetor unitário. A derivada direcional de  em
em 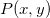 na direção de
na direção de 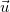 , denotada por
, denotada por 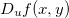 é Isto dá a taxa de variação de
é Isto dá a taxa de variação de  em relação à distância a
em relação à distância a 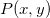 na direção definida por
na direção definida por 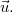
Observação 4. Se 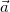 é um vetor arbitrário na mesma direção do vetor
é um vetor arbitrário na mesma direção do vetor 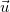 então a derivada direcional
então a derivada direcional 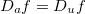 .
.
Teorema 16. Se  é uma função diferenciável de duas variáveis e
é uma função diferenciável de duas variáveis e 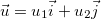 é um vetor unitário, então
é um vetor unitário, então
Prova: Consideremos  ,
,  ,
,  e
e  como valores fixos (arbitrários), e seja
como valores fixos (arbitrários), e seja  a função de uma variável definida por
a função de uma variável definida por
Pelas definições de derivadas de uma função real e derivada direcional temos
Mas considerando
onde 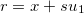 ,
, 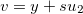 ,
, 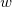 é uma função de duas variáveis
é uma função de duas variáveis  e
e  funções de uma variável
funções de uma variável  , segue então que
, segue então que
assim temos
fazendo 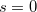 , então
, então  e
e 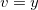 e pela primeira parte da demonstração
e pela primeira parte da demonstração
Logo,
Observação 5. As derivadas parciais primeiras de  são casos especiais da derivada direcional
são casos especiais da derivada direcional 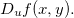 Se
Se 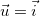 então
então 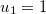 e
e 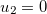 . Daí Se
. Daí Se 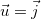 então
então
Exemplo 40. Seja  Ache a derivada direcional de
Ache a derivada direcional de  no ponto
no ponto 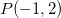 na direção do vetor
na direção do vetor 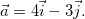
Solução: Considere o vetor 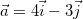 com ponto inicial
com ponto inicial 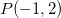 . Queremos determinar
. Queremos determinar 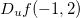 para o vetor unitário
para o vetor unitário 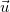 que tem a direção de
que tem a direção de 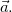 Temos que
Temos que
Como
Logo, em 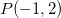
Podemos expressar a derivada direcional como segue
Definição 13. Seja  uma função de duas variáveis. O gradiente de
uma função de duas variáveis. O gradiente de  é uma função vetorial dada por
é uma função vetorial dada por
Portanto,
o símbolo 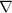 , é um operador diferencial que se define como
, é um operador diferencial que se define como
Se 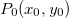 é um ponto específico do plano-xy, costuma-se denotar o vetor gradiente em
é um ponto específico do plano-xy, costuma-se denotar o vetor gradiente em 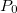 por
por  Assim
Assim
Exemplo 41. Seja 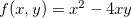 .
.
Ache o gradiente de  no ponto
no ponto 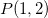 e esboce o vetor
e esboce o vetor 
Use o gradiente para achar a derivada direcional de  em
em 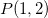 na direção de
na direção de 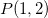 para
para 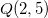 .
.
Solução: Por definição,
em 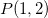 ,
,
Agora fazendo 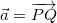 , então
, então
O vetor unitário na direção de 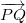 é
é
daí
Teorema 17 (do Gradiente). Seja  uma função de duas variáveis, diferenciável no ponto
uma função de duas variáveis, diferenciável no ponto 
O máximo de 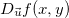 em
em 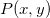 é
é 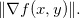
O máximo da taxa de crescimento de  em
em 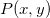 ocorre na direção de
ocorre na direção de 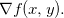
Prova: 1) Consideremos o ponto 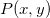 e o vetor
e o vetor  como fixos (mas arbitrários) e o vetor
como fixos (mas arbitrários) e o vetor 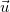 como variável. Seja
como variável. Seja 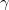 o ângulo entre
o ângulo entre 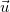 e
e 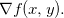 Sabemos que
Sabemos que
como 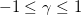 , o máximo ocorre se
, o máximo ocorre se  , neste caso,
, neste caso,  2) A derivada direcional
2) A derivada direcional 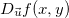 é a taxa de variação de
é a taxa de variação de  em relação à distância em
em relação à distância em 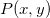 na direção definida por
na direção definida por 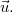 Esta taxa só atinge seu máximo se
Esta taxa só atinge seu máximo se  , isto é,
, isto é,  Neste caso,
Neste caso, 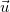 tem a mesma direção que
tem a mesma direção que 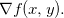
Corolário 3. Seja  uma função de duas variáveis, diferenciável no ponto
uma função de duas variáveis, diferenciável no ponto 
O mínimo de 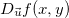 em
em 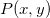 é
é 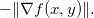
O mínimo da taxa de acréscimo (ou o máximo da taxa de decréscimo) de  em
em 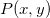 ocorre na direção de
ocorre na direção de 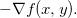
Exemplo 42. Seja 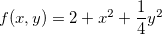 .
.
Ache a direção segundo à qual  cresce mais rapidamente no ponto
cresce mais rapidamente no ponto 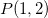 , e determine a taxa máxima de crescimento de
, e determine a taxa máxima de crescimento de  em
em 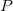 .
.
Interprete (1) utilizando o gráfico de  .
.
Solução: Pelo teorema 17 sabemos que a taxa de maior crescimento de  é a direção do gradiente de
é a direção do gradiente de  , assim
, assim
então no ponto 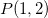 temos que
temos que
esta é a direção de maior crescimento de  no ponto
no ponto 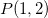 . A taxa máxima de crescimento é dada pela norma de
. A taxa máxima de crescimento é dada pela norma de 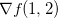 , ou seja,
, ou seja,
Para uma função  de três variáveis em
de três variáveis em 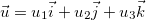 ,
, 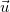 vetor unitário, temos Derivada direcional de
vetor unitário, temos Derivada direcional de 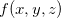 é
é
Gradiente de 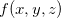 é
é
Teorema 18. Se  é uma função diferenciável de três variáveis e
é uma função diferenciável de três variáveis e  é um vetor unitário, então
é um vetor unitário, então
Observação 6. Semelhantemente ao teorema 17 (do Gradiente) temos que entre todas as derivadas direcionais possíveis 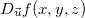 no ponto
no ponto 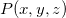 , a derivada na direção de
, a derivada na direção de 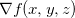 é a que tem maior valor e esse valor é
é a que tem maior valor e esse valor é 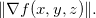
Exemplo 43. Suponhamos que um sistema coordenado  esteja localizado no espaço, de modo que a temperatura
esteja localizado no espaço, de modo que a temperatura 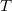 no ponto
no ponto 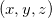 seja dada pela fórmula
seja dada pela fórmula 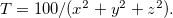
Ache a taxa de variação de 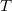 em relação à distância no ponto
em relação à distância no ponto 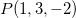 e na direção do vetor
e na direção do vetor 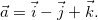
Em que direção, a partir de 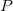 ,
, 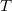 aumenta mais rapidamente? Qual a taxa máxima de variação de
aumenta mais rapidamente? Qual a taxa máxima de variação de 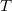 em
em 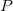 ?
?
Solução: Pela definição de gradiente, o gradiente de 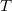 é
é
obtemos
logo,
assim
essa é a direção em que 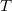 aumenta mais a partir do ponto
aumenta mais a partir do ponto 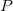 . Um vetor unitário
. Um vetor unitário 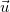 na direção de
na direção de 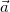 é
é
desse modo
E a taxa máxima é
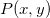 um ponto do plano e
um ponto do plano e 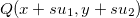 onde
onde 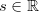 , temos então que o vetor
, temos então que o vetor 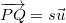 onde
onde 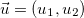 e consideramos
e consideramos 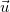 como um vetor unitário. Então
como um vetor unitário. Então ![\[ \| \overrightarrow {PQ}\| =\| s \vec{u}\| =|s|\| \vec{u}\| =|s| \]](images/img-0592.png)
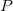 varia de
varia de 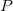 para
para 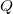 então o incremento
então o incremento 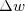 de
de 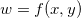 é
é ![\[ \Delta w=f(x+su_1,y+su_2)-f(x,y) \]](images/img-0593.png)
 é
é ![\[ \dfrac {\Delta w}{s}=\dfrac {f(x+su_1,y+su_2)-f(x,y)}{s}. \]](images/img-0594.png)
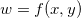 e
e 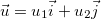 um vetor unitário. A derivada direcional de
um vetor unitário. A derivada direcional de  em
em 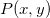 na direção de
na direção de 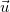 , denotada por
, denotada por 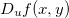 é
é ![\[ D_ u f(x,y)=\lim _{s\to 0}\dfrac {f(x+su_1,y+su_2)-f(x,y)}{s}. \]](images/img-0597.png)
 em relação à distância a
em relação à distância a 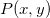 na direção definida por
na direção definida por 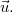
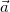 é um vetor arbitrário na mesma direção do vetor
é um vetor arbitrário na mesma direção do vetor 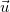 então a derivada direcional
então a derivada direcional 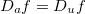 .
.  é uma função diferenciável de duas variáveis e
é uma função diferenciável de duas variáveis e 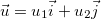 é um vetor unitário, então
é um vetor unitário, então ![\[ D_ u f(x,y)=f_ x(x,y)u_1+f_ y(x,y)u_2 \]](images/img-0601.png)
 ,
,  ,
, 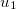 e
e  como valores fixos (arbitrários), e seja
como valores fixos (arbitrários), e seja 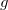 a função de uma variável definida por
a função de uma variável definida por ![\[ g(s)=f(x+su_1, y+su_2) \]](images/img-0604.png)
![\[ g’(0)=\lim _{s\to 0} \dfrac {g(s)-g(0)}{s-0} \]](images/img-0605.png)
![\[ =\lim _{s\to 0} \dfrac {f(x+su_1,y+su_2)-f(x,y)}{s} \]](images/img-0606.png)
![\[ =D_ u f(x,y) \]](images/img-0607.png)
![\[ w=g(s)=f(r,v) \]](images/img-0608.png)
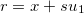 ,
, 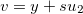 ,
, 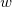 é uma função de duas variáveis
é uma função de duas variáveis  e
e  funções de uma variável
funções de uma variável  , segue então que
, segue então que ![\[ \dfrac {dw}{ds}=\dfrac {\partial w }{\partial r}\dfrac {dr}{ds}+\dfrac {\partial w }{\partial v}\dfrac {dv}{ds} \]](images/img-0613.png)
![\[ g’(s)=f_ r(r,v)u_1+f_ s(r,v)u_2 \]](images/img-0614.png)
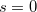 , então
, então  e
e 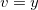 e pela primeira parte da demonstração
e pela primeira parte da demonstração ![\[ g’(0)=D_ u f(x,y). \]](images/img-0617.png)
![\[ D_ u f(x,y)=f_ x (x,y)u_1+f_ y (x,y)u_2. \]](images/img-0618.png)
 são casos especiais da derivada direcional
são casos especiais da derivada direcional 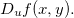 Se
Se 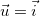 então
então 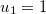 e
e 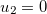 . Daí
. Daí ![\[ D_{\vec{i}} f(x,y)=f_ x(x,y). \]](images/img-0623.png)
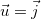 então
então ![\[ D_{\vec{j}} f(x,y)=f_ y(x,y). \]](images/img-0625.png)
 Ache a derivada direcional de
Ache a derivada direcional de  no ponto
no ponto 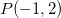 na direção do vetor
na direção do vetor 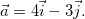
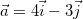 com ponto inicial
com ponto inicial 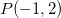 . Queremos determinar
. Queremos determinar 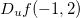 para o vetor unitário
para o vetor unitário 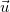 que tem a direção de
que tem a direção de 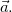 Temos que
Temos que ![\[ \vec{u}=\dfrac {1}{\| a\| }\vec{a}=\dfrac {4}{5}\vec{i}-\dfrac {3}{5}\vec{j} \]](images/img-0632.png)
![\[ f_ x(x,y)=3x^2y^2, \quad f_ y(x,y)=2x^3y \]](images/img-0633.png)
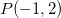
![\[ D_{\vec{u}}f(-1,2)=3(-1)^2 2^2 (\dfrac {4}{5})+2(-1)^3 2 (\dfrac {-3}{5})=12 \]](images/img-0634.png)
![\[ D_{\vec{u}}f(x,y)=[f_ x(x,y)\vec{i}+f_ y(x,y)\vec{j}]\cdot [u_1\vec{i}+u_2\vec{j}] \]](images/img-0635.png)
 uma função de duas variáveis. O gradiente de
uma função de duas variáveis. O gradiente de  é uma função vetorial dada por
é uma função vetorial dada por ![\[ \nabla f(x,y)=f_ x(x,y)\vec{i}+f_ y(x,y)\vec{j}. \]](images/img-0636.png)
![\[ D_{\vec{u}} f(x,y)=\nabla f(x,y)\cdot \vec{u} \]](images/img-0637.png)
 , é um operador diferencial que se define como
, é um operador diferencial que se define como ![\[ \nabla =\vec{i}\dfrac {\partial }{\partial x}+\vec{j}\dfrac {\partial }{\partial y} \]](images/img-0639.png)
 é um ponto específico do plano-xy, costuma-se denotar o vetor gradiente em
é um ponto específico do plano-xy, costuma-se denotar o vetor gradiente em 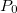 por
por  Assim
Assim ![\[ \nabla f|_{P_0}=\nabla f(x_0,y_0)=f_ x(x_0,y_0)\vec{i}+f_ y(x_0,y_0)\vec{j}. \]](images/img-0643.png)
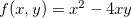 .
.  no ponto
no ponto 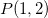 e esboce o vetor
e esboce o vetor 
 em
em 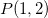 na direção de
na direção de 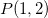 para
para 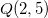 .
. ![\[ \nabla f(x,y)=(2x-4y)\vec{i}-4x\vec{j} \]](images/img-0648.png)
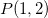 ,
, ![\[ \nabla f|_ P=\nabla f(1,2)=-6\vec{i}-4\vec{j}. \]](images/img-0649.png)
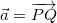 , então
, então ![\[ \vec{a}=(2-1)\vec{i}+(5-2)\vec{j}=\vec{i}+3\vec{j} \]](images/img-0651.png)
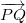 é
é ![\[ \vec{u}=\dfrac {1}{\sqrt{10}}(\vec{i}+3\vec{j}) \]](images/img-0653.png)
![\[ D_ u f(1,2)=\nabla f(1,2)\cdot \vec{u} \]](images/img-0654.png)
![\[ =(-6\vec{i}-4\vec{j})\cdot \dfrac {1}{\sqrt{10}}(\vec{i}+3\vec{j}) \]](images/img-0655.png)
![\[ =-\dfrac {6}{\sqrt{10}}-\dfrac {12}{\sqrt{10}}=-\dfrac {18}{\sqrt{10}} \]](images/img-0656.png)
 uma função de duas variáveis, diferenciável no ponto
uma função de duas variáveis, diferenciável no ponto 
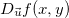 em
em 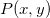 é
é 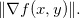
 em
em 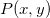 ocorre na direção de
ocorre na direção de 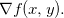
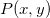 e o vetor
e o vetor  como fixos (mas arbitrários) e o vetor
como fixos (mas arbitrários) e o vetor 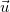 como variável. Seja
como variável. Seja 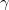 o ângulo entre
o ângulo entre 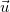 e
e 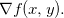 Sabemos que
Sabemos que ![\[ D_{\vec{u}}f(x,y)=\nabla f(x,y)\cdot \vec{u} \]](images/img-0663.png)
![\[ =\| \nabla f(x,y)\| \| \vec{u}\| \cos \gamma \]](images/img-0664.png)
![\[ =\| \nabla f(x,y)\| \cos \gamma \]](images/img-0665.png)
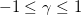 , o máximo ocorre se
, o máximo ocorre se  , neste caso,
, neste caso,  2) A derivada direcional
2) A derivada direcional 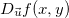 é a taxa de variação de
é a taxa de variação de  em relação à distância em
em relação à distância em 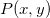 na direção definida por
na direção definida por 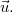 Esta taxa só atinge seu máximo se
Esta taxa só atinge seu máximo se  , isto é,
, isto é,  Neste caso,
Neste caso, 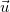 tem a mesma direção que
tem a mesma direção que 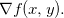
 uma função de duas variáveis, diferenciável no ponto
uma função de duas variáveis, diferenciável no ponto 
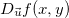 em
em 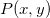 é
é 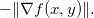
 em
em 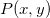 ocorre na direção de
ocorre na direção de 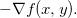
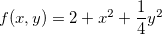 .
.  cresce mais rapidamente no ponto
cresce mais rapidamente no ponto 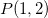 , e determine a taxa máxima de crescimento de
, e determine a taxa máxima de crescimento de  em
em 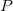 .
.  .
.  é a direção do gradiente de
é a direção do gradiente de  , assim
, assim ![\[ \nabla f(x,y)=f_ x\vec{i}+f_ y\vec{j}=2x\vec{i}+\dfrac {1}{2}y\vec{j} \]](images/img-0674.png)
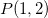 temos que
temos que ![\[ \nabla f(1,2)=2\vec{i}+\vec{j} \]](images/img-0675.png)
 no ponto
no ponto 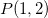 . A taxa máxima de crescimento é dada pela norma de
. A taxa máxima de crescimento é dada pela norma de 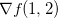 , ou seja,
, ou seja, ![\[ \| \nabla f(1,2)\| =\sqrt{2^2+1}=\sqrt{5}. \]](images/img-0677.png)
 de três variáveis em
de três variáveis em 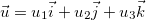 ,
, 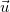 vetor unitário, temos Derivada direcional de
vetor unitário, temos Derivada direcional de 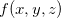 é
é ![\[ D_{\vec{u}} f(x,y,z)=\lim _{s\to 0} \dfrac {f(x+su_1, y+su_2,z+su_3)-f(x,y,z)}{s}. \]](images/img-0680.png)
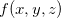 é
é ![\[ \nabla f(x,y,z)=f_ x(x,y,z)\vec{i}+f_ y(x,y,z)\vec{j}+f_ z (x,y,z)\vec{k}. \]](images/img-0681.png)
 é uma função diferenciável de três variáveis e
é uma função diferenciável de três variáveis e  é um vetor unitário, então
é um vetor unitário, então ![\[ D_{\vec{u}} f(x,y,z)=\nabla f(x,y,z)\cdot \vec{u} \]](images/img-0683.png)
![\[ =f_ x(x,y,z)u_1+f_ y(x,y,z)u_2+f_ z (x,y,z)u_3. \]](images/img-0684.png)
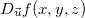 no ponto
no ponto 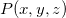 , a derivada na direção de
, a derivada na direção de 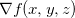 é a que tem maior valor e esse valor é
é a que tem maior valor e esse valor é 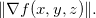
 esteja localizado no espaço, de modo que a temperatura
esteja localizado no espaço, de modo que a temperatura 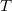 no ponto
no ponto 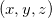 seja dada pela fórmula
seja dada pela fórmula 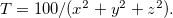
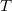 em relação à distância no ponto
em relação à distância no ponto 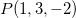 e na direção do vetor
e na direção do vetor 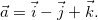
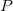 ,
, 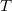 aumenta mais rapidamente? Qual a taxa máxima de variação de
aumenta mais rapidamente? Qual a taxa máxima de variação de 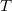 em
em 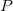 ?
? 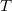 é
é ![\[ \nabla T=\dfrac {\partial T}{\partial x}\vec{i}+\dfrac {\partial T}{\partial y}\vec{j}+\dfrac {\partial T}{\partial z}\vec{k} \]](images/img-0695.png)
![\[ \dfrac {\partial T}{\partial x}=\dfrac {-200x}{(x^2+y^2+z^2)^2}, \quad \dfrac {\partial T}{\partial y}=\dfrac {-200y}{(x^2+y^2+z^2)^2} \quad \dfrac {\partial T}{\partial z}=\dfrac {-200z}{(x^2+y^2+z^2)^2} \]](images/img-0696.png)
![\[ \nabla T=\dfrac {-200}{(x^2+y^2+z^2)^2}(x\vec{i}+y\vec{j}+z\vec{k}) \]](images/img-0697.png)
![\[ \nabla T|_{P}=\dfrac {-200}{(1^2+3^2+(-2)^2)^2}(\vec{i}+3\vec{j}-2\vec{k}) \]](images/img-0698.png)
![\[ \nabla T|_ P=\dfrac {-200}{196}(\vec{i}+3\vec{j}-2\vec{k}) \]](images/img-0699.png)
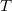 aumenta mais a partir do ponto
aumenta mais a partir do ponto 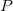 . Um vetor unitário
. Um vetor unitário 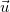 na direção de
na direção de 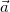 é
é ![\[ \vec{u}=\dfrac {1}{3}(\vec{i}-\vec{j}+\vec{k}) \]](images/img-0700.png)
![\[ D_{\vec{u}}|_ P=\nabla T|_ P\cdot \vec{u}=\dfrac {-200}{196}\dfrac {(1-3-2)}{\sqrt{3}}=\dfrac {200}{49\sqrt{3}}\approx 2,4 \]](images/img-0701.png)
![\[ \| \nabla T|_ P\| =\dfrac {200}{196}\sqrt{1^2+3^2+(-2)^2}=\dfrac {200}{196}\sqrt{14}\approx 3,8 \]](images/img-0702.png)