| Cálculo Diferencial e Integral 2 |
As derivadas parciais podem ser usadas para achar a derivada de funções definidas implicitamente. Suponhamos que uma equação 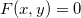 (ou
(ou  ) defina implicitamente uma função
) defina implicitamente uma função  diferenciável tal que
diferenciável tal que  , isto é,
, isto é,  , para todo
, para todo 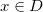 , onde
, onde 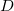 é o domínio de
é o domínio de  . Introduzimos a seguinte função composta:
. Introduzimos a seguinte função composta:
![\[ w=f(u,y) \]](images/img-0514.png) |
em que  e
e  . Temos que
. Temos que
![\[ \dfrac {dw}{dx}=\dfrac {\partial w}{\partial u}\dfrac {du}{dx}+\dfrac {\partial w}{\partial y}\dfrac {dy}{dx} \]](images/img-0516.png) |
Como 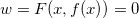 segue que
segue que 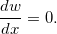 Além disso,
Além disso,  ,
, 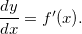 segue que
segue que
![\[ 0=\dfrac {\partial w}{\partial u}(1)+\dfrac {\partial w}{\partial y}f’(x) \]](images/img-0521.png) |
se 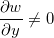 então
então
![\[ f’(x)=\dfrac {-\dfrac {\partial w}{\partial u}}{\dfrac {\partial w}{\partial y}}= \dfrac {-\dfrac {\partial w}{\partial x}}{\dfrac {\partial w}{\partial y}}=\dfrac {-F_ x(x,y)}{F_ y(x,y)} \]](images/img-0523.png) |
Teorema 14. Se uma equação 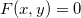 define implicitamente, uma função diferenciável
define implicitamente, uma função diferenciável  de uma variável
de uma variável  tal que
tal que  , então
, então
![\[ \dfrac {dy}{dx}=\dfrac {-F_ x(x,y)}{F_ y(x,y)}. \]](images/img-0524.png)
Exemplo 38. Ache 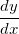 se
se  é definida implicitamente por
é definida implicitamente por
![\[ y^4+3y-4x^3-5x-1=0. \]](images/img-0526.png)
Solução: Se 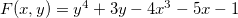 então
então 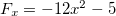 e
e 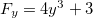 . Logo,
. Logo,
![\[ \dfrac {dy}{dx}=\dfrac {12x^2+5}{4y^3+3}. \]](images/img-0530.png) |
Dada a equação
![\[ x^2-4y^3+2z-7=0 \]](images/img-0531.png) |
podemos resolvê-la em relação a  , obtendo
, obtendo
![\[ z=\dfrac {1}{2}\left(-x^2+4y^3+7\right) \]](images/img-0532.png) |
que é da forma 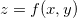 .
.
Teorema 15. Se uma equação 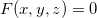 define implicitamente uma função diferenciável
define implicitamente uma função diferenciável  de duas variáveis
de duas variáveis  e
e  tais que
tais que 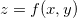 para todo
para todo 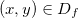 então
então
![\[ \dfrac {\partial z}{\partial x}=-\dfrac {F_ x(x,y,z)}{F_ z(x,y,z)}, \quad \dfrac {\partial z}{\partial y}=-\dfrac {F_ y(x,y,z)}{F_ z(x,y,z)}. \]](images/img-0535.png)
Prova: A equação 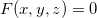 define
define 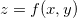 implicitamente tal que
implicitamente tal que 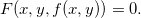 Consideremos
Consideremos
![\[ w=F(u,v,z) \]](images/img-0537.png) |
onde  ,
, 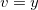 e
e 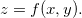 Então
Então
![\[ \dfrac {\partial w}{\partial x}=\dfrac {\partial w}{\partial u}\dfrac {\partial u}{\partial x}+\dfrac {\partial w}{\partial v}\dfrac {\partial v}{\partial x}+\dfrac {\partial w}{\partial z}\dfrac {\partial z}{\partial x} \]](images/img-0540.png) |
Mas
![\[ \dfrac {\partial u}{\partial x}=1, \quad \dfrac {\partial v}{\partial x}=0, \quad \dfrac {\partial w}{\partial x}=0 \]](images/img-0541.png) |
(já que 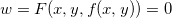 ) assim
) assim
![\[ 0=\dfrac {\partial w}{\partial x}+\dfrac {\partial w}{\partial z}\dfrac {\partial z}{\partial x} \]](images/img-0543.png) |
e se  então
então
![\[ \dfrac {\partial z}{\partial x}=-\dfrac {\partial w}{\partial x}/\dfrac {\partial w}{\partial z}=-F_ x(x,y)/F_ z(x,y). \]](images/img-0545.png) |
Exemplo 39. Ache 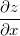 e
e 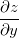 se
se 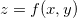 é definida implicitamente por
é definida implicitamente por
![\[ x^2 z^2+xy^2-z^3+4yz-5=0. \]](images/img-0548.png)
Solução: Seja 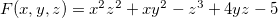 temos que
temos que
![\[ \dfrac {\partial z}{\partial x}=-\dfrac {2xz^2+y^2}{2x^2z-3z^2+4y}, \quad \dfrac {\partial z}{\partial y}=-\dfrac {2xy+4z}{2x^2z-3z^2+4y}. \]](images/img-0550.png) |