2.5.1 Regras da Cadeia
Teorema 13 (Regras da Cadeia). Se 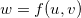 ,
, 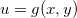 e
e 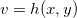 e se
e se 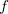 ,
, 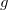 e
e 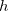 são diferenciáveis então
são diferenciáveis então
Prova: Incrementando  e mantendo
e mantendo 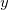 constante temos
constante temos
onde 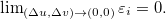
mas
temos que
com isso, concluimos que
de modo análogo se prova a outra parte do teorema.
Exemplo 34. Ache 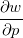 e
e 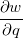 se
se
Solução: Temos que
Exemplo 35. Use a regra da cadeia para achar 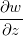 se com
se com 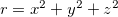 ,
, 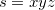 ,
, 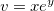 e
e 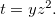
Solução:
Se 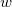 é função de duas variáveis e cada uma delas é função de uma variável
é função de duas variáveis e cada uma delas é função de uma variável 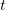 , então
, então 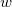 é função de
é função de 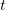 .
.
Exemplo 36. Seja 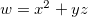 , onde
, onde 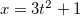 ,
, 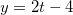 ,
, 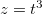 , ache
, ache 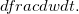
Temos pela regra da cadeia que
Exemplo 37.
Um circuito elétrico simples consiste em um resistor 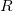 e uma força eletromotriz
e uma força eletromotriz 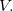 Em certo instante,
Em certo instante, 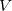 é de
é de 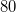 volts e aumenta à taxa de
volts e aumenta à taxa de  volts/min, enquanto
volts/min, enquanto 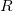 é de
é de 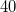 ohms e decresce à razão de
ohms e decresce à razão de 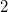 ohms/min. Use a lei de Ohm,
ohms/min. Use a lei de Ohm, 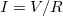 , e uma regra da cadeia, para achar a taxa à qual a corrente
, e uma regra da cadeia, para achar a taxa à qual a corrente 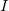 (em ampéres) varia.
(em ampéres) varia.
Solução: Como 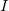 é função de
é função de 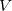 e
e 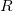 e ambos
e ambos 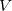 e
e 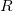 são funções do tempo
são funções do tempo 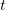 (em minutos) e aplicando a regra da cadeia,
(em minutos) e aplicando a regra da cadeia,
substituindo
assim
ampére por minuto.
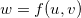 ,
, 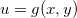 e
e 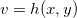 e se
e se 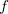 ,
, 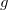 e
e 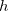 são diferenciáveis então
são diferenciáveis então ![\[ \dfrac {\partial w}{\partial x}=\dfrac {\partial w}{\partial u}\dfrac {\partial u}{\partial x}+\dfrac {\partial w}{\partial v}\dfrac {\partial v}{\partial x}; \]](images/img-0462.png)
![\[ \dfrac {\partial w}{\partial y}=\dfrac {\partial w}{\partial u}\dfrac {\partial u}{\partial y}+\dfrac {\partial w}{\partial v}\dfrac {\partial v}{\partial y}. \]](images/img-0463.png)
 e mantendo
e mantendo 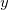 constante temos
constante temos ![\[ \Delta u=g(x+\Delta x, y)-g(x,y) \]](images/img-0464.png)
![\[ \Delta v=h(x+\Delta x, y)-h(x,y) \]](images/img-0465.png)
![\[ \Delta w=\dfrac {\partial w}{\partial u}\Delta u+\dfrac {\partial w}{\partial v}\Delta v+\varepsilon _1 \Delta u+\varepsilon _2 \Delta v \]](images/img-0466.png)
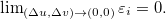
![\[ \dfrac {\Delta w}{\Delta x}=\dfrac {\partial w}{\partial u}\dfrac {\Delta u}{\Delta x}+\dfrac {\partial w}{\partial v}\dfrac {\Delta v}{\Delta x}+\varepsilon _1 \dfrac {\Delta u}{\Delta x}+\varepsilon _2 \dfrac {\Delta v}{\Delta x} \]](images/img-0468.png)
![\[ \dfrac {\partial w}{\partial x}=lim_{\Delta x \to 0}\dfrac {\Delta w}{\Delta x}, \, \dfrac {\partial u}{\partial x}=lim_{\Delta x \to 0}\dfrac {\Delta u}{\Delta x},\, \dfrac {\partial v}{\partial x}=lim_{\Delta x \to 0}\dfrac {\Delta v}{\Delta x} \]](images/img-0469.png)
![\[ \Delta u \to 0 \quad \text {quando} \quad \Delta x \to 0 \]](images/img-0470.png)
![\[ \Delta v \to 0 \quad \text {quando} \quad \Delta x \to 0 \]](images/img-0471.png)
![\[ \dfrac {\partial w}{\partial x}=\dfrac {\partial w}{\partial u}\dfrac {\partial u}{\partial x}+\dfrac {\partial w}{\partial v}\dfrac {\partial v}{\partial x}. \]](images/img-0472.png)
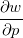 e
e 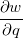 se
se ![\[ w=r^3+s^2, \quad r=pq^2, \quad s=p^2 \operatorname{sen}q. \]](images/img-0475.png)
![\[ \dfrac {\partial w}{\partial p}=\dfrac {\partial w}{\partial r}\dfrac {\partial r}{\partial p}+\dfrac {\partial w}{\partial s}\dfrac {\partial s}{\partial p} \]](images/img-0476.png)
![\[ =3r^2q^2+2s2p\operatorname{sen}q=3p^2q^6+4p^3\operatorname{sen}^2 q \]](images/img-0477.png)
![\[ \dfrac {\partial w}{\partial q}=\dfrac {\partial w}{\partial r}\dfrac {\partial r}{\partial q}+\dfrac {\partial w}{\partial s}\dfrac {\partial s}{\partial q} \]](images/img-0478.png)
![\[ =3r^2 2pq+2sp^2 \cos q=3(pq^2)2pq+2(p^2 \operatorname{sen}q) p^2 \cos q \]](images/img-0479.png)
![\[ =6p^2q^3+2p^4\operatorname{sen}q \cos q. \]](images/img-0480.png)
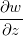 se
se ![\[ w=r^2+sv+t^3, \]](images/img-0482.png)
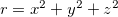 ,
, 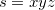 ,
, 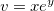 e
e 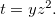
![\[ \dfrac {\partial w}{\partial z}=\dfrac {\partial w}{\partial r}\dfrac {\partial r}{\partial z}+\dfrac {\partial w}{\partial s}\dfrac {\partial s}{\partial z}+\dfrac {\partial w}{\partial v}\dfrac {\partial v}{\partial z}+\dfrac {\partial w}{\partial t}\dfrac {\partial t}{\partial z} \]](images/img-0487.png)
![\[ =2r(2z)+vxy+s0+3t^22yz \]](images/img-0488.png)
![\[ 4z(x^2+y^2+z^2)+x^2y e^ y+ 6y^3z^5. \]](images/img-0489.png)
 é função de duas variáveis e cada uma delas é função de uma variável
é função de duas variáveis e cada uma delas é função de uma variável 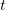 , então
, então 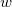 é função de
é função de 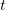 .
. 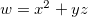 , onde
, onde 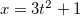 ,
, 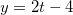 ,
, 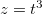 , ache
, ache 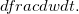
![\[ \dfrac {dw}{dt}=\dfrac {\partial w}{\partial x}\dfrac {\partial x}{\partial t}+\dfrac {\partial w}{\partial y}\dfrac {\partial y}{\partial t}+\dfrac {\partial w}{\partial z}\dfrac {\partial z}{\partial t} \]](images/img-0496.png)
![\[ \dfrac {dw}{dt}=2x(6t)+z(2)+y(3t^2)=2(3t^2+1)+2t^3+3(2t-4)t^2. \]](images/img-0497.png)
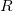 e uma força eletromotriz
e uma força eletromotriz 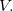 Em certo instante,
Em certo instante, 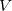 é de
é de 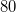 volts e aumenta à taxa de
volts e aumenta à taxa de  volts/min, enquanto
volts/min, enquanto 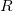 é de
é de 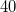 ohms e decresce à razão de
ohms e decresce à razão de 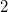 ohms/min. Use a lei de Ohm,
ohms/min. Use a lei de Ohm, 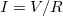 , e uma regra da cadeia, para achar a taxa à qual a corrente
, e uma regra da cadeia, para achar a taxa à qual a corrente 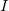 (em ampéres) varia.
(em ampéres) varia. 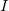 é função de
é função de 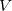 e
e 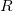 e ambos
e ambos 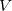 e
e 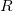 são funções do tempo
são funções do tempo 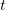 (em minutos) e aplicando a regra da cadeia,
(em minutos) e aplicando a regra da cadeia, ![\[ \dfrac {dI}{dt}=\dfrac {\partial I}{\partial V}\dfrac {dV}{dt}+\dfrac {\partial I}{\partial R}\dfrac {dR}{dt} \]](images/img-0506.png)
![\[ =\left(\dfrac {1}{R}\right)\dfrac {dV}{dt}+\left(-\dfrac {V}{R^2}\right)\dfrac {dR}{dt} \]](images/img-0507.png)
![\[ V=80, \quad \dfrac {dV}{dt}=5, \quad R=40, \dfrac {dR}{dt}=-2 \]](images/img-0508.png)
![\[ \dfrac {dI}{dt}=\left(\dfrac {1}{40}\right)5-\dfrac {80}{1600}(-2)=0,225 \]](images/img-0509.png)