| Cálculo Diferencial e Integral 2 |
Ache as derivadas parciais das funções abaixo:
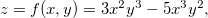
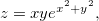
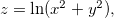
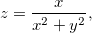
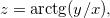
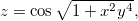
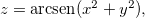
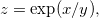
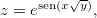
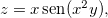
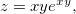
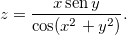
Seja 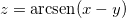 ache
ache 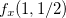 .
.
Seja 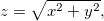 ache
ache 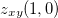 e
e 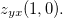
Seja. Mostre que 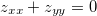 . Para as funções abaixo:
. Para as funções abaixo:
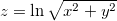 ,
,
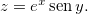
Seja 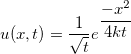 ,
, 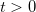 e
e 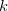 constante. Mostre que
constante. Mostre que 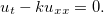
Seja 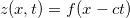 com
com 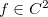 , mostre que
, mostre que 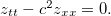
Sejam 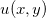 e
e 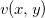 tais que
tais que 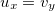 e
e 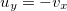 então
então 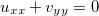 .
.
Seja 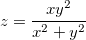 então
então 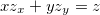 .
.
Seja 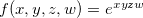 calcule
calcule 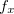 ,
, 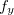 ,
, 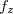 e
e 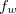 .
.
Seja