| Cálculo Diferencial e Integral 2 |
Definição 4. Seja 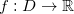 ,
, 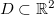 ,
, 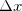 e
e 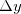 denotam o incremento de
denotam o incremento de  e
e  , respectivamente. O incremento
, respectivamente. O incremento 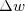 de
de 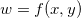 é:
é:
![\[ \Delta w=f(x+\Delta x, y+\Delta y)-f(x,y). \]](images/img-0293.png)
Exemplo 23. Seja 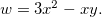 (a) se
(a) se 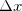 e
e 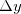 são incrementos de
são incrementos de  e
e  determine
determine 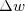 . (b) Use
. (b) Use 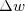 para calcular a variação de
para calcular a variação de  quando
quando 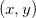 varia de
varia de 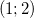 a
a 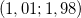 .
.
Solução: Seja
![\[ \Delta w=f(x+\Delta x,y+\Delta y)-f(x,y) \]](images/img-0297.png) |
![\[ \Delta w=3(x+\Delta x)^2-(x+\Delta x).(y+\Delta y)-(3x^2-xy) \]](images/img-0298.png) |
![\[ =3x^2+6x\Delta x+3 (\Delta x)^2-xy-x\Delta y-y\Delta x-\Delta x \Delta y-3x^2+xy \]](images/img-0299.png) |
![\[ =(6x-y)\Delta x-x\Delta y+3 (\Delta x)^2-\Delta x \Delta y \]](images/img-0300.png) |
.
Teorema 6. Seja 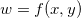 definida em
definida em 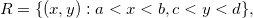 suponhamos que
suponhamos que 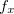 e
e 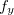 existem em
existem em  e sejam contínuas em
e sejam contínuas em 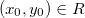 . Se
. Se 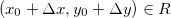 e
e 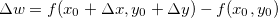 então
então
onde
![\[ \Delta w=f_ x(x_0,y_0)\Delta x+f_ y(x_0,y_0)\Delta y+ \varepsilon _1 \Delta x+\varepsilon _2 \Delta y \]](images/img-0306.png)
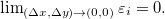
Definição 5. Seja As bluediferenciais A bluediferencial da variável dependente 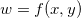 e sejam
e sejam 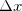 e
e 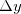 incrementos de
incrementos de  e
e  , respectivamente.
, respectivamente.
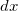 e
e 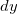 das variáveis independentes
das variáveis independentes  e
e  são
são 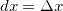 e
e 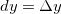 .
.  é
é
![\[ dw=f_ x(x,y)dx+f_ y(x,y)dy. \]](images/img-0313.png)
Exemplo 24. Se 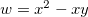 calcule
calcule 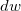 .
.
Solução:
![\[ dw=\dfrac {\partial w}{\partial x}dx+\dfrac {\partial w}{\partial y}dy \]](images/img-0316.png) |
![\[ dw=(6x-y)dx+(-x)dy \]](images/img-0317.png) |
.
Definição 6. Seja 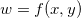 a função
a função  é bluediferenciável em
é bluediferenciável em 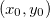 se
se 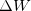 puder ser escrita como:
puder ser escrita como:
onde
![\[ \Delta w=f_ x(x_0,y_0)\Delta x+f_ y(x_0,y_0)\Delta y+ \varepsilon _1 \Delta x+\varepsilon _2\Delta y \]](images/img-0320.png)
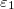 e
e 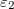 são funções de
são funções de 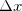 e
e 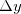 e
e 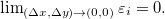
Diz-se que uma função  é bluediferenciável numa região
é bluediferenciável numa região  se
se  é diferenciável em todos os pontos de
é diferenciável em todos os pontos de  .
.
Teorema 7. Seja 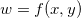 e se
e se 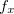 e
e 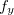 são contínuas numa região
são contínuas numa região  então
então  diferenciável em
diferenciável em  .
.
Prova: Consequência do teorema  .
.
Teorema 8. Se uma função  é diferenciável em
é diferenciável em 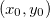 então ela é contínua nesse ponto.
então ela é contínua nesse ponto.
Prova:
![\[ \Delta w=f(x_0+\Delta x, y_0+\Delta y)-f(x_0,y_0) \]](images/img-0324.png) |
![\[ \Delta w=f_ x(x_0,y_0)\Delta x+f_ y(x_0,y_0)\Delta y+ \varepsilon _1 \Delta x+\varepsilon _2 \Delta y. \]](images/img-0325.png) |
Fazendo 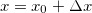 e
e 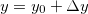 obtemos
obtemos
![\[ f(x,y)-f(x_0,y_0)=f_ x(x_0,y_0)(x-x_0)+f_ y(x_0,y_0)(y-y_0)+ \varepsilon _1 (x-x_0)+\varepsilon _2 (y-y_0), \]](images/img-0328.png) |
segue que
![\[ \lim _{(x,y)\rightarrow (x_0,y_0)} f(x,y)-f(x_0,y_0)=0 \]](images/img-0329.png) |
logo  é contínua.
é contínua.
Corolário 1. Se  é uma função de duas variáveis e se
é uma função de duas variáveis e se 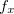 e
e 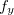 são contínuas numa região retangular
são contínuas numa região retangular  então
então  é contínua em
é contínua em  .
.
Prova: Segue diretamente do teorema 8.
Exemplo 25. Seja
Então
![\[ f(x,y)=\begin{cases} \dfrac {xy}{x^2+y^2}\, (x,y)\neq (0,0)\\ 0, \, (x,y)=(0,0) \end{cases} \]](images/img-0330.png)
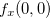 ,
, 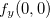 existem;
existem;  não é contínua em
não é contínua em 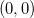 ;
;  não é diferenciável em
não é diferenciável em 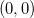 .
.
De fato, temos que
![\[ f_ x(0,0)=\lim _{h\to 0} \dfrac {f(h,0)-f(0,0)}{h}=\lim _{h\to 0}\dfrac {\dfrac {h.0}{h^2+0^2}-0}{h}=0. \]](images/img-0334.png) |
Analogamente, 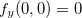 , portanto, essas derivadas parciais de
, portanto, essas derivadas parciais de  existem no ponto
existem no ponto 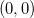 mas, nota-se que elas não são contínuas na origem. Também vemos que
mas, nota-se que elas não são contínuas na origem. Também vemos que
![\[ \lim _{x\to 0} f(x,x)=\lim _{x \to 0} \dfrac {x^2}{2x^2}=\dfrac {1}{2} \]](images/img-0336.png) |
o que implica que  não é contínua na origem, logo
não é contínua na origem, logo  não pode ser diferenciável.
não pode ser diferenciável.
Seja 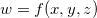 uma função de três variáveis então seu incremento será
uma função de três variáveis então seu incremento será
![\[ \Delta w=f(x+\Delta x, y+\Delta y,z+\Delta z)-f(x,y,z). \]](images/img-0337.png) |
e também teremos que
![\[ \Delta w=f_ x(x,y,z)\Delta x+f_ y (x,y,z)\Delta y+f_ z (x,y,z)\Delta z+ \varepsilon _1 \Delta x+\varepsilon _2 \Delta y+\varepsilon _3 \Delta z \]](images/img-0338.png) |
onde 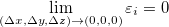 .
.
Definição 7. Seja 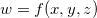 as diferenciais de
as diferenciais de  ,
,  e
e  são:
são:
e a diferencial de
![\[ dx=\Delta x, \quad dy=\Delta y, \quad dz=\Delta z \]](images/img-0340.png)
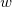 é:
é:
![\[ dw=\frac{\partial w}{\partial x}dx+\frac{\partial w}{\partial y}dy+\frac{\partial w}{\partial z}dz. \]](images/img-0341.png)
Exemplo 26. Suponha que as dimensões de uma caixa retangular varia de Obtenha uma aproximação da variação do volume. Ache a variação exata do volume. 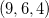 para
para 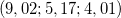 .
.
onde 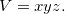
Solução:(a) 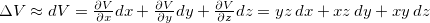
![\[ dV=0,98-1,08+0,54=-0,06 \]](images/img-0346.png) |
(b)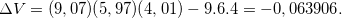
Suponhamos 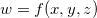 definida numa região
definida numa região  do espaço tridimensional e suponha que existam
do espaço tridimensional e suponha que existam 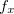 ,
, 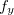 e
e 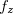 em
em  e que sejam contínuas em
e que sejam contínuas em 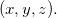 Se dermos a
Se dermos a  ,
,  ,
,  incrementos
incrementos 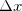 ,
, 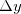 ,
, 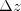 , respectivamente, então o incremento de
, respectivamente, então o incremento de 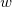 correspondente é:
correspondente é:
![\[ \Delta w=f(x+\Delta x, y+\Delta y, z+\Delta z)-f(x,y,z). \]](images/img-0350.png) |
Podemos escrever este incremento na forma:
![\[ \Delta w=\dfrac {\partial f}{\partial x}(x,y,z)\Delta x+\dfrac {\partial f}{\partial y}(x,y,z)\Delta y+\dfrac {\partial f}{\partial z}(x,y,z)\Delta z+R(\Delta x, \Delta y,\Delta z), \]](images/img-0351.png) |
onde 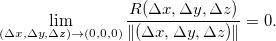
Definição 8. Seja As diferenciais A diferencial 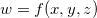 e sejam
e sejam 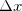 ,
, 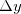 e
e 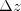 incrementos de
incrementos de  ,
,  e
e  , respectivamente.
, respectivamente.
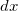 ,
, 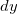 e
e 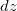 de
de  ,
,  e
e  são
são
![\[ dx=\Delta x, \quad dy=\Delta y, \quad dz=\Delta z. \]](images/img-0354.png)
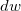 da variável dependente
da variável dependente 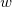 é
é
![\[ dw=\dfrac {\partial w}{\partial x}dx+\dfrac {\partial w}{\partial y}dy+\dfrac {\partial w}{\partial z}dz. \]](images/img-0355.png)
Pode-se usar 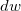 como aproximação de
como aproximação de 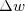 se os incrementos de
se os incrementos de  ,
,  e
e  são pequenos.
são pequenos.
Definição 9. Seja 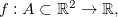
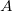 aberto, e
aberto, e 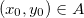 . Dizemos que
. Dizemos que  é diferenciável em
é diferenciável em 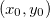 se, e somente se, existirem reais
se, e somente se, existirem reais  e
e 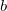 tais que
tais que
![\[ \lim _{(h,k)\to (0,0)} \dfrac {f(x_0+h,y_0+k)-f(x_0,y_0)-a\cdot h-b\cdot k}{\| (h,k)\| }=0. \]](images/img-0358.png)
Observação 2. Podíamos também definir a diferenciabilidade de  em
em 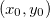 como:
como:
onde
![\[ f(x_0+h,y_0+k)=f(x_0,y_0)+a\cdot h+b\cdot k+R(h,k) \]](images/img-0359.png)
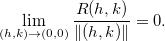
Teorema 9.
Se  for diferenciável em
for diferenciável em 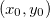 então
então  é contínua em
é contínua em 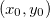 .
.
Prova: Sendo  diferenciável em
diferenciável em 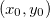 , existem reais
, existem reais  e
e 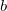 tais que
tais que
![\[ \lim _{(h,k)\to (0,0)} \dfrac {R(h,k)}{\| (h,k)\| }=0 \]](images/img-0361.png) |
onde 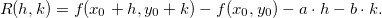 Como
Como 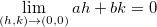 e
e 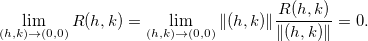 resulta que
resulta que  é contínua em
é contínua em  .
.
Teorema 10. Seja 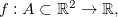
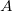 aberto, e
aberto, e 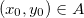 . Se
. Se  for diferenciável nesse ponto, então
for diferenciável nesse ponto, então  admitirá derivadas parciais nesse ponto.
admitirá derivadas parciais nesse ponto.
Prova: Seja  diferenciável no ponto
diferenciável no ponto 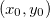 então existem
então existem  e
e 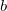 tais que
tais que
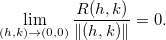 |
(2.5) |
onde 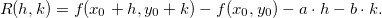 Segue de (2.5) que
Segue de (2.5) que
![\[ \lim _{h\to 0} \dfrac {R(h,0)}{\| (h,0)\| }=\lim _{h\to 0} \dfrac {f(x_0+h,y_0)-f(x_0,y_0)-a\cdot h}{|h|}=0 \]](images/img-0366.png) |
ou
![\[ \lim _{h\to 0}\dfrac {f(x_0+h,y_0)-f(x_0,y_0)-a\cdot h}{h}=0 \]](images/img-0367.png) |
e, portanto,
![\[ \dfrac {\partial f}{\partial x}(x_0,y_0)=\lim _{h\to 0}\dfrac {f(x_0+h,y_0)-f(x_0,y_0)}{h}=a \]](images/img-0368.png) |
Analogamente,
![\[ \dfrac {\partial f}{\partial y}(x_0,y_0)=b. \]](images/img-0369.png) |
Teorema 11. Seja 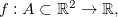
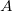 aberto, e
aberto, e 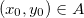 . Tem-se que
. Tem-se que  é diferenciável em
é diferenciável em 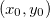 se, e somente se,
se, e somente se,  admite derivadas parciais em
admite derivadas parciais em 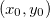 e
e 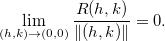
Observação 3. Devemos notar que as seguintes condições devem ser satisfeitas para a diferenciabilidade de uma função Se uma das derivadas parciais em Se Se  :
:
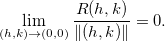
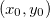 não existem então
não existem então  não é diferenciável.
não é diferenciável. 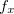 e
e 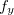 existem em
existem em 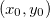 mas o item 1 não é satisfeito então
mas o item 1 não é satisfeito então  não é diferenciável.
não é diferenciável.  não é contínua então
não é contínua então  não é diferenciável.
não é diferenciável.
Exemplo 27. Mostre que a função 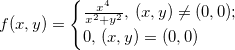 é uma função diferenciável.
é uma função diferenciável.
Solução: Temos que
![\[ \dfrac {\partial f}{\partial x}=\begin{cases} \dfrac {2x^5+4x^3y^2}{(x^2+y^2)^2}, \, (x,y)\neq (0,0);\\ 0, \, (x,y)=(0,0) \end{cases} \]](images/img-0372.png) |
e
![\[ \dfrac {\partial f}{\partial y}=\begin{cases} \dfrac {-2x^4 y}{(x^2+y^2)^2}, \, (x,y)\neq (0,0);\\ 0, \, (x,y)=(0,0) \end{cases} \]](images/img-0373.png) |
Em 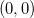 temos que
temos que
![\[ \dfrac {\partial f}{\partial x} (0,0)=\lim _{(x,y)\to (0,0)} \dfrac {\partial f}{\partial x} (x,y)=\lim _{(x,y)\to (0,0)}\dfrac {2x^5+4x^3y^2}{(x^2+y^2)^2}=0; \]](images/img-0374.png) |
o mesmo vale para 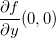 , logo
, logo  é diferenciável.
é diferenciável.
Exemplo 28. Considere a função: 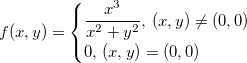 é diferenciável em
é diferenciável em 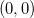 ?
?
Solução|:
![\[ \dfrac {\partial f}{\partial x}(0,0)=1, \]](images/img-0377.png) |
![\[ \dfrac {\partial f}{\partial y}(0,0)=0 \]](images/img-0378.png) |
Como
![\[ R(h,k)=f(h,k)-f(0,0)-\dfrac {\partial f}{\partial x}(0,0)h+\dfrac {\partial f}{\partial y}|(0,0)k \]](images/img-0379.png) |
então,
![\[ R(h,k)=\dfrac {h^3}{h^2+k^2}-h \]](images/img-0380.png) |
logo,
![\[ \dfrac {R(h,k)}{\| (h,k)\| }=-\dfrac {hk^2}{(h^2+k^2)\sqrt{h^2+k^2}}=G(h,k) \]](images/img-0381.png) |
assim,
![\[ \lim _{t \to 0} G(t,t)=-\lim _{t \to 0}\dfrac {t}{2\sqrt{2} |t|} \]](images/img-0382.png) |
esse limite não existe, o que implica que o limite
![\[ \lim _{(h,k)\to (0,0)}\dfrac {R(h,k)}{\| (h,k)\| } \]](images/img-0383.png) |
não existe. Portanto,  não é diferenciável. Note que
não é diferenciável. Note que  é contínua, pois,
é contínua, pois,
![\[ \lim _{(x,y)\to (0,0)} f(x,y)=\lim _{(x,y)\to (0,0)} x\left(\dfrac {x^2}{x^2+y^2}\right)=0. \]](images/img-0384.png) |
Exemplo 29. A função
é diferenciável em
![\[ f(x,y)=\begin{cases} \dfrac {yx^2}{x^4+y^2}, \, (x,y)\neq (0,0)\\ 0, \, (x,y)=(0,0) \end{cases} \]](images/img-0385.png)
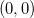 ?
?
Solução:  não é contínua em
não é contínua em 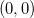 , logo não é diferenciável.
, logo não é diferenciável.