| Cálculo Diferencial e Integral 2 |
Teorema 12. Seja 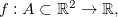
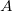 aberto, e
aberto, e 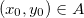 . Se as derivadas parciais
. Se as derivadas parciais 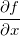 e
e 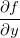 existirem em
existirem em 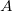 e forem contínuas em
e forem contínuas em 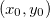 então
então  é diferenciável nesse ponto.
é diferenciável nesse ponto.
Prova: Como 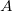 é aberto então existe uma bola aberta centrada no ponto
é aberto então existe uma bola aberta centrada no ponto 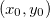 contida em
contida em 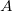 , isto é,
, isto é, 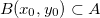 , logo,
, logo, 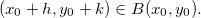 Temos que
Temos que
![\[ f(x_0+h,y_0+k)-f(x_0,y_0)=f(x_0+h,y_0+k)-f(x_0,y_0+k)+f(x_0,y_0+k)-f(x_0,y_0). \]](images/img-0390.png) |
Chamando 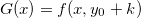 então pelo Teorema do valor médio(T.V.M.), temos que
então pelo Teorema do valor médio(T.V.M.), temos que
![\[ G(x_0+h)-G(x_0)=G’(\xi )h=\dfrac {\partial f}{\partial x}(\xi , y_0+k)h \]](images/img-0392.png) |
onde 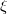 está entre
está entre 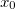 e
e 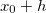 . Analogamente, definindo
. Analogamente, definindo 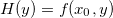 então pelo T.V.M.
então pelo T.V.M.
![\[ H(y_0+k)-H(y_0)=H’(\eta )k=\dfrac {\partial f}{\partial y}(x_0,\eta )k \]](images/img-0397.png) |
onde 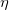 está entre
está entre 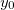 e
e 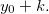 Assim
Assim
![\[ f(x_0+h,y_0+k)-f(x_0,y_0)-\dfrac {\partial f}{\partial x}(x_0, y_0)h-\dfrac {\partial f}{\partial y}(x_0, y_0)h= \]](images/img-0401.png) |
![\[ =\left[\dfrac {\partial f}{\partial x}(\xi , y_0+k)-\dfrac {\partial f}{\partial x}(x_0, y_0)\right]h+\left[\dfrac {\partial f}{\partial y}(x_0, \eta )-\dfrac {\partial f}{\partial y}(x_0, y_0)\right]k \]](images/img-0402.png) |
como as derivadas parciais de  são contínuas, segue que o limite do lado direito da igualdade acima vai pra zero quando
são contínuas, segue que o limite do lado direito da igualdade acima vai pra zero quando 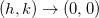 , pois,
, pois, 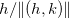 e
e 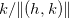 são limitadas.
são limitadas.
Definição 10. Uma função  diz-se de classe
diz-se de classe 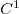 se
se 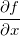 e
e 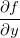 forem contínuas em
forem contínuas em 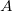 . Uma função
. Uma função  é de classe
é de classe 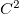 se
se 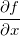 ,
, 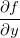 ,
, 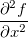 ,
, 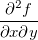 ,
, 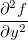 forem contínuas. De um modo geral, uma função
forem contínuas. De um modo geral, uma função  é de classe
é de classe 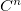 se
se 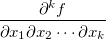 forem contínuas com
forem contínuas com 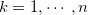 , e onde os
, e onde os 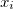 podem, eventualmente, ser repetidos e iguais a
podem, eventualmente, ser repetidos e iguais a  e(ou)
e(ou)  . E, finalmente, uma função
. E, finalmente, uma função  diz-se de classe
diz-se de classe 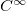 se ela é de classe
se ela é de classe 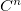 para todo
para todo 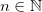 .
.
Corolário 2. Seja 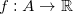 ,
, 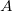 aberto. Se
aberto. Se  é de classe
é de classe 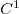 então
então  é diferenciável.
é diferenciável.
Exemplo 30. Seja 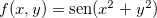 .
.  é de classe
é de classe 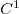 , pois
, pois 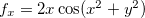 e
e 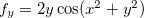 que são contínuas no
que são contínuas no 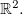
Exemplo 31. Seja
![\[ f(x,y)=\begin{cases} (x^2+y^2)\operatorname{sen}\dfrac {1}{x^2+y^2}, \, (x,y)\neq (0,0)\\ 0, \, (x,y)=(0,0) \end{cases} \]](images/img-0422.png)
 é diferenciável, mas
é diferenciável, mas 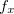 e
e 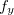 não são contínuas em
não são contínuas em 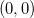 .
.
De fato,
![\[ f_ x(0,0)=lim_{h\to 0} \dfrac {f(h,0)-f(0,0)}{h} \]](images/img-0423.png) |
![\[ =\lim _{h\to 0} h^2 \operatorname{sen}\frac{1}{h^2}=0 \]](images/img-0424.png) |
e 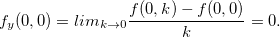 Mas
Mas
![\[ f_ x(x,y)=2x \operatorname{sen}\dfrac {1}{x^2+y^2}+(x^2+y^2) \dfrac {(-2x)}{(x^2+y^2)^2}\cos \dfrac {1}{x^2+y^2} \]](images/img-0426.png) |
![\[ =2x\left( \operatorname{sen}\dfrac {1}{x^2+y^2}-\dfrac {1}{x^2+y^2}\cos \dfrac {1}{x^2+y^2}\right) \]](images/img-0427.png) |
não é contínua na origem. Analogamente, 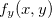 não é contínua na origem.
não é contínua na origem.