2.1 Derivadas Parciais
Definição 3. Se  é uma função de duas variáveis, as bluederivadas parciais de
é uma função de duas variáveis, as bluederivadas parciais de  em relação a
em relação a  e a
e a  são as funções
são as funções 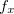 e
e 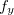 definidas por e desde que existam os limites.
definidas por e desde que existam os limites.
Notações:
se 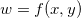 então
então
Exemplo 18. Calcule 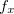 e
e 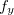 se
se 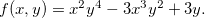
Solução: Temos que:
Exemplo 19. Seja 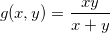 ache
ache 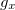 e
e 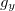 .
.
Solução: A derivada parcial 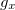 é:
é:
de modo análogo, temos que 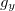 é:
é:
Observação 1. Se  representa a temperatura em cada ponto
representa a temperatura em cada ponto 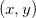 , então
, então  é a variação líquida da temperatura,
é a variação líquida da temperatura, 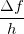 é a variação média da temperatura e
é a variação média da temperatura e 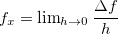 é a taxa instantânea de variação da temperatura em relação à distância quando
é a taxa instantânea de variação da temperatura em relação à distância quando 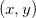 se move na direção
se move na direção 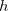 .
.
blueInterpretação geométrica das derivadas parciais
Considere os pontos 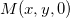 e
e 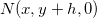 . O plano
. O plano  paralelo ao plano-yz, passando por
paralelo ao plano-yz, passando por 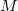 e
e 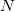 intercepta uma curva
intercepta uma curva 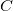 paralela ao plano-yz, na direção do eixo-y. Sejam
paralela ao plano-yz, na direção do eixo-y. Sejam 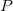 e
e 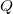 pontos dessa curva
pontos dessa curva 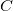 que projetados no plano-xy dão
que projetados no plano-xy dão 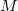 e
e 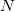 , respectivamente. Conforme a figura 2.1,
, respectivamente. Conforme a figura 2.1, 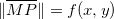 e
e 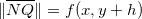 e
e 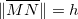 . A razão
. A razão ![$[f(x,y+h)-f(x,y)]/h$](images/img-0254.png) é o coeficiente angular da secante por
é o coeficiente angular da secante por  e
e  no plano
no plano 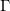 . O limite desta razão quando
. O limite desta razão quando 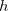 tende a zero, ou seja,
tende a zero, ou seja, 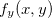 , é o coeficiente angular da tangente a
, é o coeficiente angular da tangente a 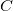 , na direção do eixo-y. Analogamente, temos a interpretação para
, na direção do eixo-y. Analogamente, temos a interpretação para 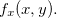
Para a função de três variáveis, definimos as derivadas parciais do mesmo modo, isto é, se  é função de três variáveis
é função de três variáveis  ,
,  e
e  , então
, então
e
Exemplo 20. Se 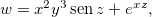 determine
determine 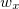 ,
, 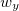 e
e 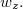
Solução: Temos que
Se  é função de duas variáveis
é função de duas variáveis  e
e  então
então 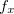 e
e 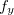 são também funções das duas variáveis
são também funções das duas variáveis  e
e  ; podemos então considerar as suas derivadas parciais primeiras, que serão as bluederivadas parciais segundas de
; podemos então considerar as suas derivadas parciais primeiras, que serão as bluederivadas parciais segundas de  e denotamos:
e denotamos:
Exemplo 21. Determine as derivadas parciais segundas de  se
se 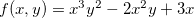 .
.
Solução: Vimos que
daí
Exemplo 22. Considere a função
Note que
logo,
daí
Portanto, 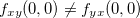 . Mas, se uma função
. Mas, se uma função 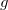 têm derivadas parciais segundas contínuas, então
têm derivadas parciais segundas contínuas, então 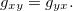 De maneira análoga se define as derivadas parciais terceiras (ou de terceira ordem), ou de ordem superior. Por exemplo,
De maneira análoga se define as derivadas parciais terceiras (ou de terceira ordem), ou de ordem superior. Por exemplo,
Se as derivadas parciais de terceira ordem forem contínuas então
De forma análoga se define as derivadas parciais segundas e de ordem superior para as funções 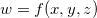 de três variáveis.
de três variáveis.
 é uma função de duas variáveis, as bluederivadas parciais de
é uma função de duas variáveis, as bluederivadas parciais de  em relação a
em relação a  e a
e a  são as funções
são as funções 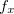 e
e 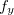 definidas por
definidas por ![\[ f_ x(x,y)=\lim _{h\to 0} \dfrac {f(x+h,y)-f(x,y)}{h} \]](images/img-0230.png)
![\[ f_ y(x,y)=\lim _{k\to 0} \dfrac {f(x,y+k)-f(x,y)}{k} \]](images/img-0231.png)
![\[ f_ x=\dfrac {\partial f}{\partial x}, \quad f_ y=\dfrac {\partial f}{\partial y} \]](images/img-0232.png)
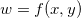 então
então ![\[ f_ x=\dfrac {\partial f}{\partial x}=\dfrac {\partial w}{\partial x}=w_ x \]](images/img-0234.png)
![\[ f_ y=\dfrac {\partial f}{\partial y}=\dfrac {\partial w}{\partial y}=w_ y \]](images/img-0235.png)
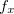 e
e 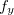 se
se 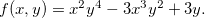
![\[ f_ x(x,y)=2xy^4-9x^2y^2 \]](images/img-0237.png)
![\[ f_ y(x,y)=4x^2y^3-6x^3y+3. \]](images/img-0238.png)
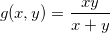 ache
ache 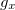 e
e 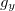 .
. 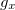 é:
é: ![\[ g_ x=\dfrac {y(x+y)-xy}{(x+y)^2}=\dfrac {y^2}{(x+y)^2} \]](images/img-0242.png)
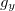 é:
é: ![\[ g_ y=\dfrac {x(x+y)-xy}{(x+y)^2}=\dfrac {x^2}{(x+y)^2}. \]](images/img-0243.png)
 representa a temperatura em cada ponto
representa a temperatura em cada ponto 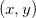 , então
, então  é a variação líquida da temperatura,
é a variação líquida da temperatura, 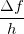 é a variação média da temperatura e
é a variação média da temperatura e 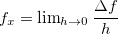 é a taxa instantânea de variação da temperatura em relação à distância quando
é a taxa instantânea de variação da temperatura em relação à distância quando 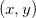 se move na direção
se move na direção 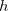 .
. 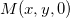 e
e 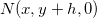 . O plano
. O plano 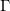 paralelo ao plano-yz, passando por
paralelo ao plano-yz, passando por 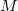 e
e 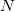 intercepta uma curva
intercepta uma curva 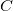 paralela ao plano-yz, na direção do eixo-y. Sejam
paralela ao plano-yz, na direção do eixo-y. Sejam 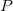 e
e 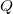 pontos dessa curva
pontos dessa curva 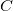 que projetados no plano-xy dão
que projetados no plano-xy dão 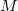 e
e 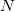 , respectivamente. Conforme a figura 2.1,
, respectivamente. Conforme a figura 2.1, 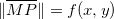 e
e 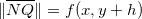 e
e 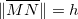 . A razão
. A razão ![$[f(x,y+h)-f(x,y)]/h$](images/img-0254.png) é o coeficiente angular da secante por
é o coeficiente angular da secante por  e
e  no plano
no plano 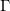 . O limite desta razão quando
. O limite desta razão quando 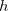 tende a zero, ou seja,
tende a zero, ou seja, 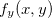 , é o coeficiente angular da tangente a
, é o coeficiente angular da tangente a 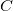 , na direção do eixo-y. Analogamente, temos a interpretação para
, na direção do eixo-y. Analogamente, temos a interpretação para 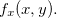
![\includegraphics[scale=1]{interpreta.eps}](images/img-0257.png)
 é função de três variáveis
é função de três variáveis  ,
,  e
e  , então
, então ![\[ f_ x=\lim _{h\to 0} \dfrac {f(x+h,y,z)-f(x,y,z)}{h}, \]](images/img-0258.png)
![\[ f_ y=\lim _{h\to 0} \dfrac {f(x,y+h,z)-f(x,y,z)}{h}, \]](images/img-0259.png)
![\[ f_ z=\lim _{h\to 0} \dfrac {f(x,y,z+h)-f(x,y,z)}{h}. \]](images/img-0260.png)
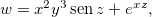 determine
determine 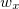 ,
, 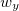 e
e 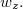
![\[ w_ x=2xy^3\operatorname{sen}z+ze^{xz}, \]](images/img-0265.png)
![\[ w_ y=3x^2y^2 \operatorname{sen}z+0, \]](images/img-0266.png)
![\[ w_ z=x^2y^3 \cos z+xe^{xz}. \]](images/img-0267.png)
 é função de duas variáveis
é função de duas variáveis  e
e  então
então 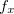 e
e 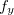 são também funções das duas variáveis
são também funções das duas variáveis  e
e  ; podemos então considerar as suas derivadas parciais primeiras, que serão as bluederivadas parciais segundas de
; podemos então considerar as suas derivadas parciais primeiras, que serão as bluederivadas parciais segundas de  e denotamos:
e denotamos: ![\[ \dfrac {\partial f_ x}{\partial x}=(f_ x)_ x=f_{xx}=\dfrac {\partial }{\partial x}\left(\dfrac {\partial f}{\partial x}\right)=\dfrac {\partial ^2 f}{\partial x^2} \]](images/img-0268.png)
![\[ \dfrac {\partial f_ x}{\partial y}=(f_ x)_ y=f_{xy}=\dfrac {\partial }{\partial y}\left(\dfrac {\partial f}{\partial x}\right)=\dfrac {\partial ^2 f}{\partial y\partial x} \]](images/img-0269.png)
![\[ \dfrac {\partial f_ y}{\partial x}=(f_ y)_ x=f_{yx}=\dfrac {\partial }{\partial x}\left(\dfrac {\partial f}{\partial y}\right)=\dfrac {\partial ^2 f}{\partial x\partial y} \]](images/img-0270.png)
![\[ \dfrac {\partial f_ y}{\partial y}=(f_ y)_ y=f_{yy}=\dfrac {\partial }{\partial y}\left(\dfrac {\partial f}{\partial y}\right)=\dfrac {\partial ^2 f}{\partial y^2} \]](images/img-0271.png)
 se
se 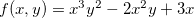 .
. ![\[ f_ x=3x^2y^2-4xy+3 \]](images/img-0273.png)
![\[ f_ y=2x^3y-2x^2 \]](images/img-0274.png)
![\[ f_{xx}=6xy^2-4y \]](images/img-0275.png)
![\[ f_{xy}=6x^2y-4x=f_{yx} \]](images/img-0276.png)
![\[ f_{yy}=2x^3 \]](images/img-0277.png)
![\[ f(x,y)=\begin{cases} \dfrac {xy(x^2-y^2)}{x^2+y^2}, \quad x^2+y^2\neq 0\\ 0, \quad x^2+y^2=0 \end{cases} \]](images/img-0278.png)
![\[ f_ x(x,y)=\dfrac {x^4y+4x^2y^3-y^5}{(x^2+y^2)^2}, \quad f_ x(x,y)=\dfrac {x^5-4xy^4}{(x^2+y^2)^2} \]](images/img-0279.png)
![\[ f_ x(0,y)=-y, \quad f_ y(x,0)=x \]](images/img-0280.png)
![\[ f_{xy}(0,0)=-1, \quad f_{yx}(0,0)=1 \]](images/img-0281.png)
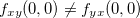 . Mas, se uma função
. Mas, se uma função  têm derivadas parciais segundas contínuas, então
têm derivadas parciais segundas contínuas, então 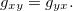 De maneira análoga se define as derivadas parciais terceiras (ou de terceira ordem), ou de ordem superior. Por exemplo,
De maneira análoga se define as derivadas parciais terceiras (ou de terceira ordem), ou de ordem superior. Por exemplo, ![\[ \dfrac {\partial f_{xx}}{\partial x}=f_{xxx}=\dfrac {\partial }{\partial x}\left(\dfrac {\partial ^2 f}{\partial x^2}\right)=\dfrac {\partial ^3 f}{\partial x^3} \]](images/img-0284.png)
![\[ \dfrac {\partial f_{xy}}{\partial x}=f_{xyx}=\dfrac {\partial }{\partial x}\left(\dfrac {\partial ^2 f}{\partial y \partial x}\right)=\dfrac {\partial ^3 f}{\partial x \partial y \partial x} \]](images/img-0285.png)
![\[ f_{xyx}=f_{yxx}=f_{xxy}. \]](images/img-0286.png)
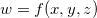 de três variáveis.
de três variáveis. ![\[ w_{xx}=\dfrac {\partial ^2 f}{\partial x^2}, \quad w_{xy}=\dfrac {\partial ^2 f}{\partial y \partial x}, \quad w_{xz}= \dfrac {\partial ^2 f}{\partial z \partial x}, \]](images/img-0288.png)
![\[ w_{yy}=\dfrac {\partial ^2 f}{\partial y^2},\quad w_{yz}=\dfrac {\partial ^2 f}{\partial z \partial y},\quad w_{zz}=\dfrac {\partial ^2 f}{\partial z^2}. \]](images/img-0289.png)