| Cálculo Diferencial e Integral 2 |
Definição 2. Seja 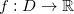 uma função de duas variáveis com domínio
uma função de duas variáveis com domínio 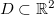 . Dizemos que
. Dizemos que  tem limite
tem limite 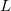 quando
quando 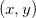 se aproxima de
se aproxima de 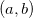 e, denotamos por
e, denotamos por 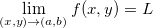 se, dado
se, dado 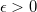 , existe
, existe 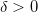 tal que se
tal que se 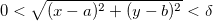 então
então
![\[ |f(x,y)-f(a,b)|<\epsilon . \]](images/img-0089.png)
Essa definição quer dizer que quando um ponto 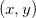 se aproxima do ponto
se aproxima do ponto 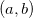 no plano-xy então o valor
no plano-xy então o valor  se aproxima do valor de
se aproxima do valor de  . Podemos provar que quando esse limite existe, ele é único.
. Podemos provar que quando esse limite existe, ele é único.
Propriedade 1 (Propriedades do Limite). Sejam Se  e
e 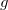 funções de duas variáveis tais que
funções de duas variáveis tais que 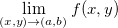 e
e 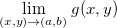 existam e sejam iguais a
existam e sejam iguais a 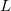 e
e 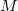 , respectivamente, e tome
, respectivamente, e tome  constante. Então,
constante. Então,
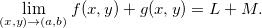
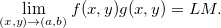
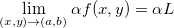
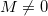 então
então 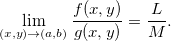
A função polinomial é definida por
![\[ P(x,y)=\sum _{m=0}^{s} \sum _{n=0}^{r} a_{nm}x^ n y^ m. \]](images/img-0100.png) |
A função racional é definida por
![\[ R(x,y)=\dfrac {P(x,y)}{Q(x,y)} \]](images/img-0101.png) |
onde 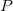 e
e 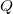 são funções polinomiais.
são funções polinomiais.
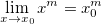
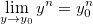
Assim: 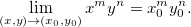
Logo: 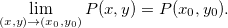
Se 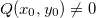 então
então 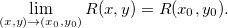
Exemplo 6. Ache o limite de:
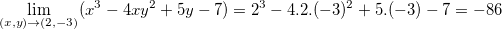 .
. 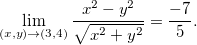
Exemplo 7. O 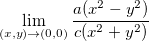 não existe, onde
não existe, onde  e
e  são reais positivos e não nulos.
são reais positivos e não nulos.
De fato, Note que 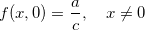 e
e 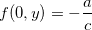 assim,
assim, 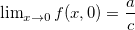 e
e 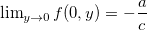 , logo o limite
, logo o limite 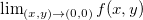 não pode existir. Qualquer círculo centrado na origem tem sempre valores de
não pode existir. Qualquer círculo centrado na origem tem sempre valores de  iguais a
iguais a  e valores iguais a
e valores iguais a 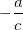 , temos que dado
, temos que dado 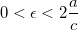 , podemos achar
, podemos achar 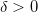 com
com 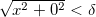 tal que
tal que 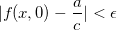 mas
mas 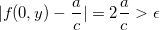 .
.
Teorema 1. Se dois caminhos diferentes para um ponto 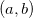 resulta em dois limites diferentes então
resulta em dois limites diferentes então 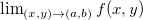 não existe.
não existe.
Veja que no exemplo 7 anterior, o limite da função 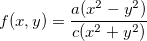 nao existe pois tomando os eixos (eixo-x e eixo-y) coordenados os limites são diferentes.
nao existe pois tomando os eixos (eixo-x e eixo-y) coordenados os limites são diferentes.
Exemplo 8. Mostre que o 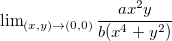 não existe, com
não existe, com  e
e 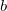 reais diferentes de zero.
reais diferentes de zero.
Solução: Ao longo da reta 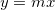 temos:
temos:
![\[ \lim _{x \to 0} \dfrac {ax^2 (mx)}{b(x^4+m^2 x^2)}=\lim _{x\to 0} \dfrac {amx^3}{b(x^4+m^2x^2)} \]](images/img-0131.png) |
![\[ =\lim _{x\to 0}\dfrac {amx}{b(x^2+m^2)}=\dfrac {0}{b(0+m^2)}=0. \]](images/img-0132.png) |
Ao longo da parábola:
![\[ \lim _{x\to 0} \dfrac {ax^2x^2}{b(x^4+(x^2)^2}=\lim _{x\to 0}\dfrac {ax^4}{2bx^4}=\dfrac {a}{2b}. \]](images/img-0133.png) |
Seja 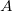 um subconjunto do espaço bidimensional
um subconjunto do espaço bidimensional 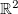 . Um ponto
. Um ponto 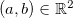 é blue ponto interior de
é blue ponto interior de 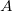 se existe uma bola aberta
se existe uma bola aberta 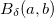 com centro em
com centro em 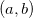 inteiramente contida em
inteiramente contida em 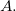 a bola aberta
a bola aberta 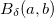 é definida por
é definida por
![\[ B_{\delta }(a,b)=\{ (x,y)\in \mathbb {R}^2: (x-a)^2+(y-b)^2<\delta ^2\} \]](images/img-0137.png) |
![\[ B_{\delta }(a,b)\subset A \]](images/img-0138.png) |
![\includegraphics[scale=1.5]{pontint.png}](images/img-0139.png)
Uma blueregião aberta 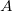 é uma região onde todos os seus pontos são pontos interiores. Um ponto
é uma região onde todos os seus pontos são pontos interiores. Um ponto 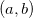 é um blue ponto de fronteira de
é um blue ponto de fronteira de 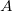 se dada qualquer bola aberta
se dada qualquer bola aberta 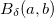 então ela contém pontos de
então ela contém pontos de 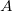 e pontos fora de
e pontos fora de 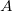 . Uma região
. Uma região 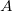 é bluefechada quando contém todos os seus pontos fronteira. Temos que
é bluefechada quando contém todos os seus pontos fronteira. Temos que 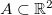 ou
ou 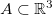 é blue aberto se todos os seus pontos são pontos interiores.
é blue aberto se todos os seus pontos são pontos interiores. 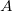 é blue fechado se, e somente se,
é blue fechado se, e somente se, 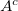 é aberto.
é aberto.
Exemplo 9.
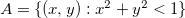 é aberto.
é aberto. 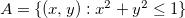 é fechado.
é fechado.