| Cálculo Diferencial e Integral 2 |
Seja 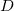 um subconjunto aberto do
um subconjunto aberto do 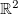 e seja
e seja 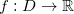 . A função
. A função 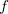 é bluecontínua num ponto
é bluecontínua num ponto 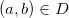 se
se
![\[ \lim _{(x,y)\to (a,b)} f(x,y)=f(a,b). \]](images/img-0146.png) |
Exemplo 10. O polinômio é uma função contínua, isto é,
é contínua, pois, já vimos que
![\[ P(x,y)=\sum _{i=0}^ n \sum _{j=0} a_{ij} x^ i y^ j \]](images/img-0147.png)
![\[ \lim _{(x,y)\to (a,b)}P(x,y)=P(a,b). \]](images/img-0148.png)
Exemplo 11.
A função
![\[ f(x,y)=\begin{cases} \dfrac {x^2-y^2}{x-y}, \quad (x,y)\neq (0,0)\\ 0, \quad (x,y)=(0,0) \end{cases} \]](images/img-0149.png) |
é descontínua em 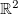 , pois,
, pois,
![\[ \dfrac {x^2-y^2}{x-y} \]](images/img-0150.png) |
não está definida na reta 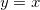 . Mas se definimos
. Mas se definimos
![\[ f(x,y)=\begin{cases} \dfrac {x^2-y^2}{x-y}, \quad (x,y)\neq (0,0)\\ 2x, \quad (x,y)=(x,x) \end{cases} \]](images/img-0152.png) |
então essa nova função é contínua, já que,
![\[ \lim _{(x,y)\to (x,x)} \dfrac {x^2-y^2}{x-y}=\lim _{(x,y)\to (x,x)} x+y=2x. \]](images/img-0153.png) |
Exemplo 12. A função
é contínua no
![\[ f(x,y)=\begin{cases} \dfrac {x^2 y}{x^2+y^2}, \quad (x,y)\neq (0,0)\\ 0, \quad (x,y)=(0,0) \end{cases} \]](images/img-0154.png)
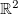 .
.
Solução: Só precisamos mostrar a continuidade na origem. (Por quê?) Assim,
![\[ 0\leq \lim _{(x,y)\to (0,0)} |f(x,y)|=\lim _{(x,y)\to (0,0)} \dfrac {|x|^2|y|}{x^2+y^2}\leq \lim _{(x,y)\to (0,0)}\dfrac {|x|(x^2+y^2)}{x^2+y^2}=0. \]](images/img-0155.png) |
Logo,
![\[ \lim _{(x,y)\to (0,0)} |f(x,y)|=\lim _{(x,y)\to (0,0)} f(x,y)=0. \]](images/img-0156.png) |
o que prova a continuidade de 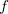 .
.
Vamos estabelecer agora alguns resultados importantes que podem ser usados na resolução de diversos problemas.
Teorema 2. Sejam 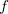 ,
, 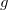 e
e 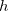 funções de duas variáveis com interseção nos seus domínios. Suponha que um ponto
funções de duas variáveis com interseção nos seus domínios. Suponha que um ponto 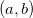 pertença a essa interseção, se
pertença a essa interseção, se 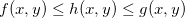 e
e 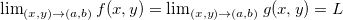 então
então 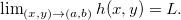
Teorema 3. Temos que o 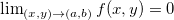 se, e somente se,
se, e somente se, 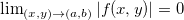
Teorema 4. Sejam 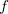 e
e 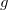 funções de duas variáveis com o mesmo domínio
funções de duas variáveis com o mesmo domínio 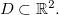 Se
Se 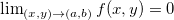 e
e 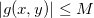 para todo
para todo 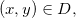 então
então 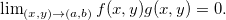
Propriedade 2 (Propriedades do Limite). Sejam Se 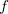 e
e 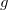 funções de duas variáveis contínuas no ponto
funções de duas variáveis contínuas no ponto 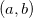 e tome
e tome  constante. Então,
constante. Então,
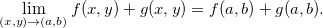
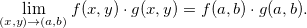
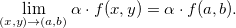
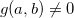 então
então 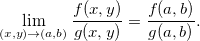
Exemplo 13. A função
é descontínua na origem.
![\[ f(x,y)=\begin{cases} \dfrac {x^2 y}{x^2+y^2}, \quad (x,y)\neq (0,0)\\ 1, \quad (x,y)=(0,0) \end{cases} \]](images/img-0172.png)
Exemplo 14. A função
é contínua no domínio
![\[ f(x,y)= \dfrac {x^2 y}{x^2+y^2}, \quad (x,y)\neq (0,0) \]](images/img-0173.png)
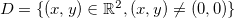 .
.
Exemplo 15. A função
é descontínua no domínio
![\[ f(x,y)= \dfrac {x^2 y}{x^2+y^2}, \]](images/img-0175.png)
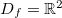 , pois
, pois 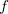 não é contínua na origem.
não é contínua na origem.
Uma função 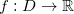 com
com 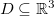 é bluecontínua num ponto
é bluecontínua num ponto 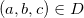 se
se
![\[ \lim _{(x,y,z)\to (a,b,c)} f(x,y,z)=f(a,b,c). \]](images/img-0179.png) |
Um exemplo bem simples de uma função contínua de três variáveis são as funções polinomiais, isto é,
![\[ P(x,y,z)=\sum _{n=0}^ N \sum _{m=0}^ M \sum _{p=0}^ P a_{nmp}x^ n y^ m z^ p. \]](images/img-0180.png) |