| Cálculo Diferencial e Integral 2 |
Definição 1. Seja 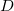 um subconjunto de
um subconjunto de 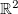 . Uma função
. Uma função  de duas variáveis é uma função tal que
de duas variáveis é uma função tal que
![\[ f: D \rightarrow \mathbb {R}, \quad D\subset \mathbb {R}^2 \]](images/img-0004.png)
onde
![\[ (x,y)\mapsto f(x,y) \]](images/img-0005.png)
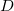 é o domínio de
é o domínio de  .
.
O domínio 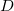 de uma função
de uma função  é o conjunto de elementos do
é o conjunto de elementos do 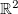 tal que
tal que  faz sentido. A imagem de
faz sentido. A imagem de  é o conjunto de todos os números reais
é o conjunto de todos os números reais  com
com 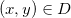 , isto é,
, isto é,
![\[ Im(f)=\{ f(x,y)\in \mathbb {R}, \quad (x,y)\in D\} . \]](images/img-0008.png) |
![\includegraphics[scale=1]{funcvv.png}](images/img-0009.png)
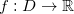
Exemplo 1. Se 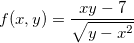 . Determine o domínio de
. Determine o domínio de  .
.
Solução: O domínio de  é o conjunto dos pontos
é o conjunto dos pontos 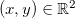 tal que
tal que 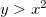 .
.
![\includegraphics[scale=1]{cilindro.png}](images/img-0014.png)
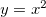
Seja 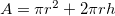 então
então 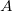 é a área de um cilindro circular reto em função do raio
é a área de um cilindro circular reto em função do raio  e da altura
e da altura 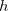 .
.  e
e 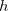 são as variáveis independentes e
são as variáveis independentes e 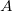 é a variável dependente.
é a variável dependente.
![\includegraphics[scale=1]{yx2.png}](images/img-0020.png)
De modo análogo, se  é um subconjunto de
é um subconjunto de  , definimos
, definimos 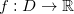 tal que
tal que 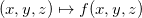 ,
,  é uma função de três variáveis
é uma função de três variáveis  ,
,  e
e  . Neste caso,
. Neste caso, 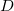 é uma região do espaço tridimensional e é o domínio de
é uma região do espaço tridimensional e é o domínio de  , a imagem de
, a imagem de  é
é
![\[ Im(f)=\{ f(x,y,z): (x,y,z)\in D\} \subset {\mathbb {R}} \]](images/img-0027.png) |
![\[ D=\{ (x,y,z): f(x,y,z) \quad \textsf{faz sentido}\} \subset {\mathbb {R}} \]](images/img-0028.png) |
Seja 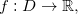 com
com 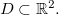 O gráfico de
O gráfico de  é, por definição, o gráfico da superfície
é, por definição, o gráfico da superfície  determinada pela equação,
determinada pela equação, 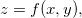 num sistema de coordenadas
num sistema de coordenadas 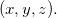 Isto é, o conjunto
Isto é, o conjunto
![\[ S=Graf(f(x,y))=\{ (x,y,z): (x,y)\in D_ f\quad \text {e}\quad z=f(x,y)\} \]](images/img-0034.png) |
é o gráfico de 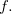
Exemplo 2. Seja
Esboce o gráfico de
![\[ f(x,y)=9-x^2-y^2, \quad D=\{ (x,y): x^2+y^2\leq 9\} . \]](images/img-0036.png)
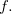
O domínio de  é o disco
é o disco 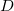 que está dentro do círculo de raio 3, inclusive o próprio círculo. Temos que
que está dentro do círculo de raio 3, inclusive o próprio círculo. Temos que
![\[ z=9-x^2-y^2, \quad z+x^2+y^2=9 \quad \textsf{equação do parabolóide} \]](images/img-0037.png) |
Se fazemos 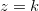 obtemos curvas no plano
obtemos curvas no plano 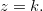 Seja
Seja  uma função de duas variáveis e consideremos o traço do gráfico de
uma função de duas variáveis e consideremos o traço do gráfico de  no plano
no plano 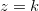 . Projetando este traço no plano-xy obtemos uma curva
. Projetando este traço no plano-xy obtemos uma curva 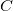 de equação
de equação 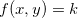 ,
, 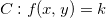 é a bluecurva de nível
é a bluecurva de nível 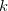 de
de  .
.
Exemplo 3. Esboce algumas curvas de nível da função  do exemplo 2.
do exemplo 2.
Solução: Quando fazemos 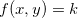 , obtemos
, obtemos 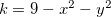 ou
ou 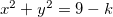 com
com 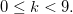 Ou seja obtemos círculos.
Ou seja obtemos círculos.
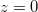 , temos que
, temos que 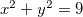 obtemos o círculo de raio
obtemos o círculo de raio 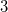 .
.
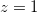 , temos que
, temos que  obtemos o círculo de raio
obtemos o círculo de raio 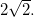
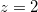 , temos que
, temos que 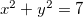 obtemos o círculo de raio
obtemos o círculo de raio 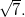
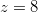 , temos que
, temos que 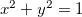 obtemos o círculo de raio
obtemos o círculo de raio  .
.
Se  é uma função de três variáveis então
é uma função de três variáveis então 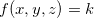 são bluesuperfícies de nível
são bluesuperfícies de nível 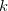 de
de 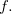
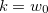 então
então 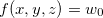 é o gráfico de uma superfície
é o gráfico de uma superfície  .
.
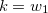 então
então 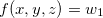 é o gráfico de uma superfície
é o gráfico de uma superfície 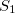 .
.
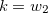 então
então 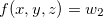 é o gráfico de uma superfície
é o gráfico de uma superfície 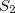 .
.
Exemplo 4. Seja 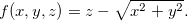
Faça 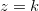 , obtemos
, obtemos 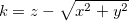 ou
ou 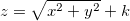 . Para cada
. Para cada 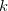 teremos um cone circular reto com vértice ao longo do eixo-z.
teremos um cone circular reto com vértice ao longo do eixo-z.
Exemplo 5. Seja 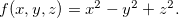
tomando 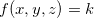 temos
temos
![\[ x^2-y^2+z^2=k, \quad k\in \mathbb {R}. \]](images/img-0073.png) |
consideremos a seguinte tabela:
Valor de |
Superfície de nível |
Descrição da superfície |
|
|
Hiperbolóide de uma folha ao longo do eixo-y |
|
|
Cone na direção do eixo-y |
|
|
Hiperbolóide de duas folhas ao longo do eixo-y |
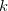 de
de 