| Cálculo Diferencial e Integral 2 |
Seja 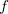 uma função diferenciável, isto é,
uma função diferenciável, isto é,
![\[ f(x_0+h, y_0+k)=f(x_0,y_0)+\dfrac {\partial f}{\partial x}(x_0,y_0)h+\dfrac {\partial f}{\partial y}(x_0,y_0)k+R(h,k) \]](images/img-0429.png) |
onde 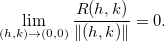 Fazendo
Fazendo 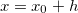 e
e 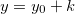 e chamando
e chamando 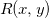 o erro que se comete ao aproximarmos
o erro que se comete ao aproximarmos 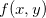 por
por
![\[ T(x,y)=f(x_0,y_0)+\dfrac {\partial f}{\partial x}(x_0,y_0)(x-x_0)+\dfrac {\partial f}{\partial y}(x_0,y_0)(y-y_0) \]](images/img-0433.png) |
então
![\[ f(x,y)=T(x,y)+R(x,y) \]](images/img-0434.png) |
onde 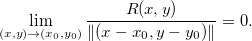
Definição 11. Sejam 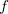 diferenciável no ponto
diferenciável no ponto 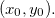 O Plano
O Plano
é o plano tangente ao gráfico de
![\[ z-f(x_0,y_0)=\dfrac {\partial f}{\partial x}(x_0,y_0)(x-x_0)+\dfrac {\partial f}{\partial y}(x_0,y_0)(y-y_0) \]](images/img-0437.png)
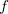 no ponto
no ponto 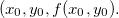
![\includegraphics[scale=1]{superfi.eps}](images/img-0439.png)
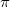
O vetor normal ao plano tangente é o vetor:
![\[ \vec{\eta }=(\dfrac {\partial f}{\partial x}(x_0,y_0),\dfrac {\partial f}{\partial y}(x_0,y_0), -1) \]](images/img-0441.png) |
então a reta normal ao plano tangente ou à superfície determinada por 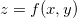 é
é
![\[ (x,y,z)=(x_0,y_0, f(x_0,y_0))+\lambda (\dfrac {\partial f}{\partial x}(x_0,y_0),\dfrac {\partial f}{\partial y}(x_0,y_0), -1), \, \lambda \in \mathbb {R} \]](images/img-0443.png) |
Exemplo 32. Seja 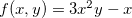 , ache o plano tangente e a reta normal à superfície determinada por
, ache o plano tangente e a reta normal à superfície determinada por 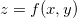 no ponto
no ponto 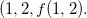
Solução: Pelo que vimos anteriormente, temos que 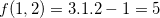
![\[ \dfrac {\partial f}{\partial x}(x,y)=6xy-1 \]](images/img-0447.png) |
logo
![\[ \dfrac {\partial f}{\partial x}(1,2)=6.1.2-1=11 \]](images/img-0448.png) |
analogamente,
![\[ \dfrac {\partial f}{\partial y}(x,y)=3x^2 \]](images/img-0449.png) |
assim
![\[ \dfrac {\partial f}{\partial x}(1,2)=3.1=3 \]](images/img-0450.png) |
portanto, o plano tangente é:
![\[ z-5=11(x-1)+3(y-2) \]](images/img-0451.png) |
ou
![\[ 11x+3y-z=12 \]](images/img-0452.png) |
e a reta normal é:
![\[ (x,y,z)=(1,2,5)+\lambda (11, 3, -1) \]](images/img-0453.png) |
ou
![\[ \begin{cases} x=1+11\lambda ,\\ y=2+3\lambda ,\\ z=5-\lambda \end{cases} \]](images/img-0454.png) |