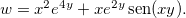| Cálculo Diferencial e Integral 2 |
Sejam  uma função de duas variáveis
uma função de duas variáveis  e
e  e
e  uma função de uma variável
uma função de uma variável 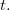 Pode-se obter uma função
Pode-se obter uma função 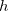 de duas variáveis definida por
de duas variáveis definida por 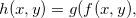 desde que a imagem de
desde que a imagem de 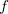 esteja no domínio de
esteja no domínio de 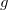 . Isto é,
. Isto é, 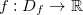 ,
, 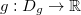 e
e 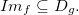
![\includegraphics[scale=1.5]{composicao.png}](images/img-0186.png)
Exemplo 16. Expresse 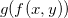 em termos de
em termos de  e
e 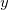 e ache o domínio da função resultante.
e ache o domínio da função resultante.
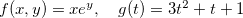 .
. 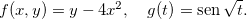
Solução:
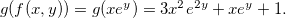
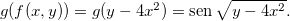
O domínio para a primeira composição é o  e o domínio para a segunda composição é o conjunto
e o domínio para a segunda composição é o conjunto  definido por
definido por 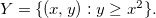
Temos o seguinte teorema em relação a continuidade da composição de funções.
Teorema 5. Se uma função 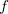 de duas variáveis é contínua em
de duas variáveis é contínua em 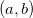 e uma função
e uma função 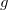 de uma variável é contínua em
de uma variável é contínua em 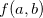 então a função
então a função 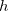 definida por
definida por 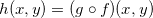 é contínua em
é contínua em 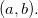
Prova: Como 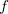 é contínua, dado
é contínua, dado 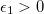 , existe
, existe 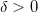 tal que se
tal que se 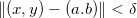 então
então 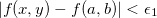 . E dado
. E dado 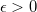 ,
, 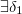 tal que se
tal que se 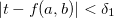 então
então 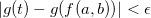 . Para
. Para 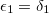 existe
existe 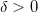 tal que se
tal que se 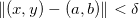 então
então 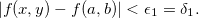 Segue que
Segue que
![\[ |h(x,y)-h(a,b)|=|g(f(x,y))-g(f(a,b))|<\epsilon . \]](images/img-0207.png) |
Logo, 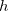 é contínua em
é contínua em 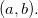
Exemplo 17. Se 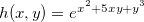 então
então 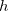 é contínua em
é contínua em 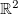 , pois é a composição da função exponencial
, pois é a composição da função exponencial 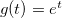 e a função polinomial
e a função polinomial 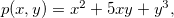 ambas contínuas, ou seja,
ambas contínuas, ou seja, 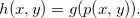
Podemos também considerar o seguinte tipo de composição: seja 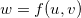 , onde
, onde 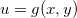 e
e 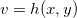 com
com 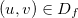 então
então 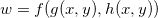 . Por exemplo, seja,
. Por exemplo, seja, 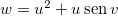 , onde
, onde 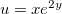 e
e 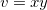 , temos então que
, temos então que