Cálculo Diferencial e Integral 2
Cálculo Diferencial e Integral 2 : Funções de Várias Variáveis : Exercícios da primeira seção

1.5 Exercícios da primeira seção

  1. A função

      \[ f(x,y)=\begin{cases} \dfrac {xy}{x^2+y^2} \quad (x,y)\neq (0,0)\\ 0 \quad (x,y)=(0,0) \end{cases} \]    

    é contínua na origem?

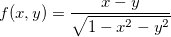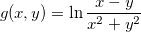  2. Analise sobre o domínio das funções $f(x,y)=\dfrac {x-y}{\sqrt{1-x^2-y^2}}$ e $g(x,y)=\ln \dfrac {x-y}{x^2+y^2}$.

  3. Descreva os domínios das funções abaixo:

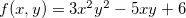
    1. $f(x,y)=3x^2 y^2-5xy+6$

  4. Analise sobre a continuidade da função

      \[ f(x,y)=\begin{cases} e^{\frac{1}{x^2+y^2-1}}, \quad x^2+y^2<1\\ 0, \quad x^2+y^2\geq 1 \end{cases} \]    

  5. A função

      \[ f(x,y)=\begin{cases} \dfrac {x-3y}{x^2+y^2}, \quad (x,y)\neq (0,0)\\ 0, \quad (x,y)=(0,0) \end{cases} \]    

    é contínua na origem?

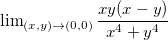  6. O limite $\lim _{(x,y)\to (0,0)} \dfrac {xy(x-y)}{x^4+y^4}$ existe?

Cálculo Diferencial e Integral 2