No espaço tridimensional, um ponto de coordenadas (x, y, z) pode ser girado em torno de um dos eixos coordenados bastando para isso que ele multiplicado por uma matriz de rotação.

As matrizes de rotação de um ângulo q em torno dos eixos x, y e z, respectivamente, são dadas por P_x(q), P_y(q) e P_z(q):

Uma maneira interessante de projetar pontos do R³ no plano R² é através de duas rotações de ângulos q e f em torno dos eixos y e z, respectivamente, seguidas da projeção no plano y0z definida por

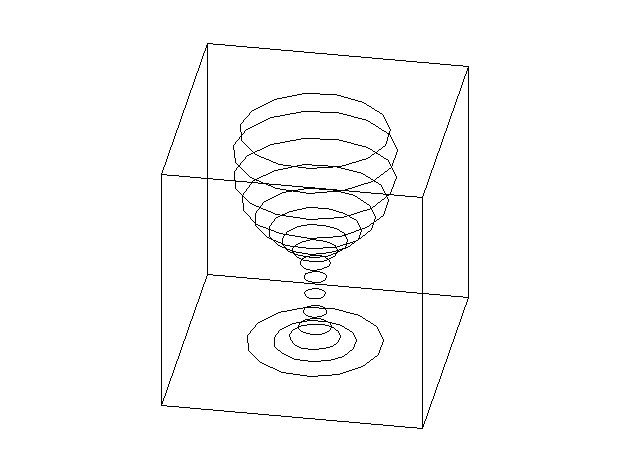
Podemos utilizar o que foi dito anteriormente para representar objetos tridimensionais no plano (por exemplo, na tela do computador) e, depois, girá-los à vontade na tela. Isso foi feito nos dois exemplos a seguir, com um ``ônibus espacial'' e com uma ``taça''. Por isso, as transformações lineares têm grandes aplicações em Computação Gráfica.

Exemplo 1:

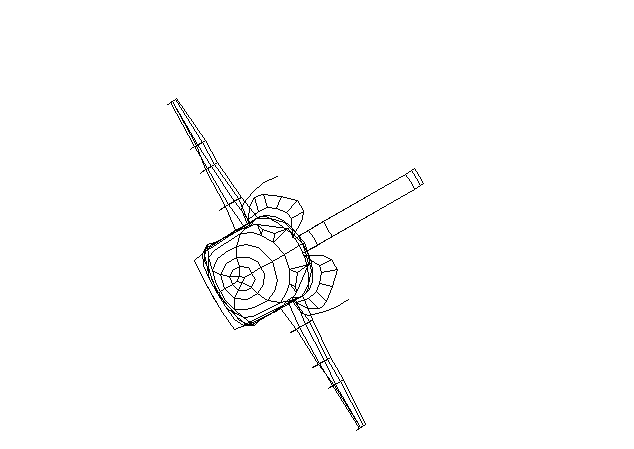
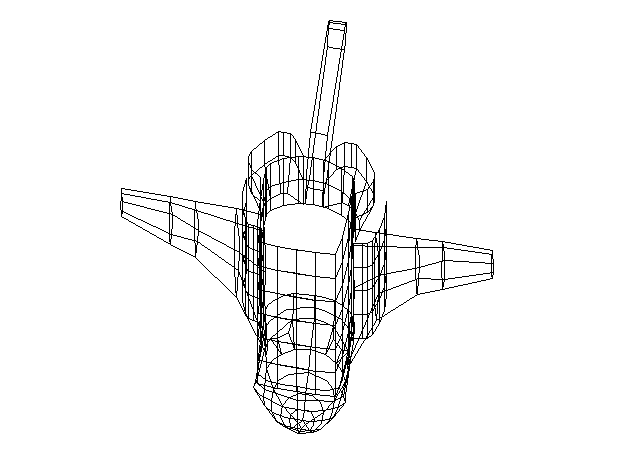
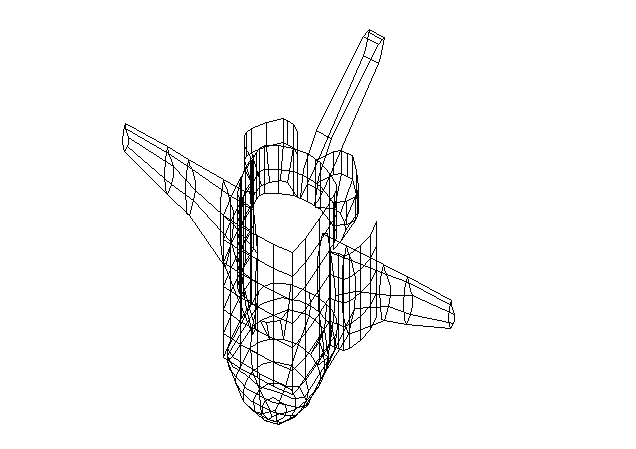
Exemplo 2:

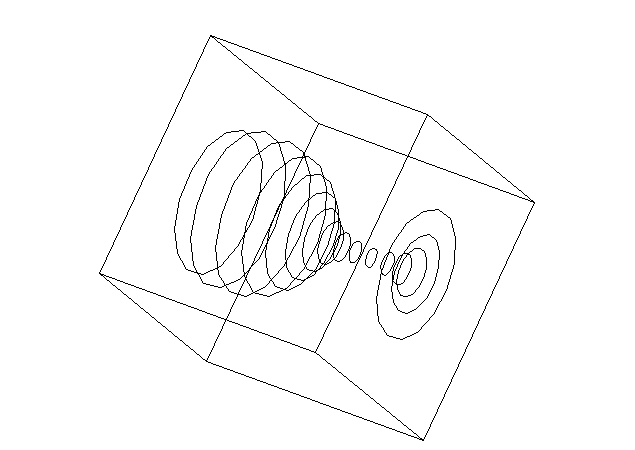
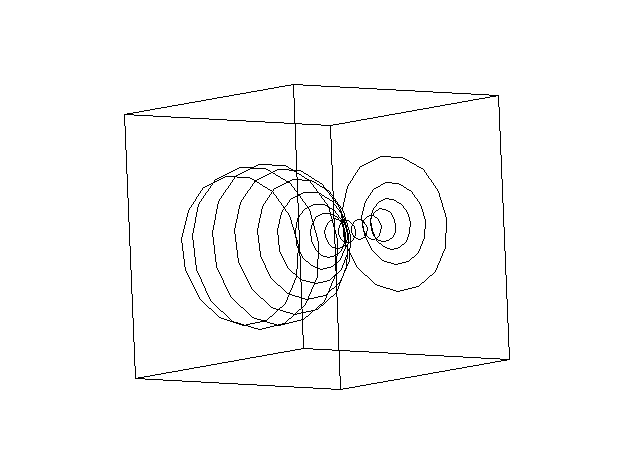
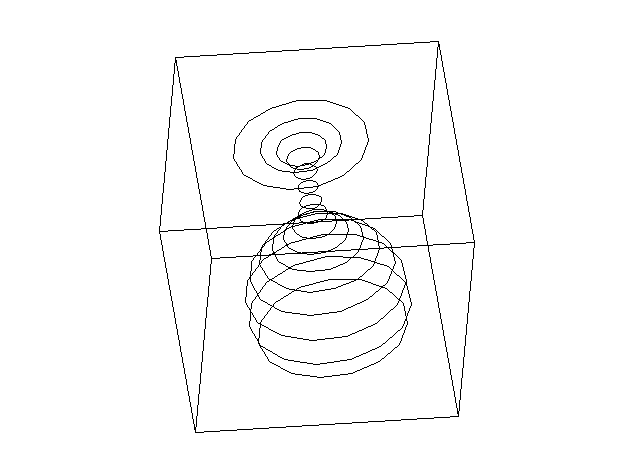
O programa para MS-DOS utilizado para gerar as figuras acima pode ser copiado pressionando-se aqui (552 Kbytes). A forma de usar é muito simples: no prompt do MS-DOS basta digitar o nome do programa (3DVISION) seguido de um nome de figura (arquivo de dados de extensão .3DV). Por exemplo,