MATHEMATICA

MATHEMATICA

A primeira versão do MATHEMATICA surgiu em 1988. Fabricado pela Wolfram Research, possui centenas de funções e recursos voltados para a resolução de problemas matemáticos. Além da enorme eficiência do programa, chama a atenção o forte esquema de comercialização: existem centenas de livros, artigos em jornais e revistas enaltecendo os recursos do programa e uma infinidade de programas auxiliares (todos vendidos separadamente, é claro!). É um programa de Computação Algébrica (calcula analiticamente limites, derivadas, integrais, ...) munido de muitos recursos numéricos e gráficos.

A seguir, algumas funções do MATHEMATICA. Para cada funçãomostrada, foi anexado pelo menos um exemplo. As linhas que iniciam com um In[] são os comandos digitados pelo usuário e as iniciadas com um Out[] são as respostas do programa. Todafunção pré-definida do programa deve iniciar com letramaiúscula e os argumentos das funções devem estar entre colchetes. Por exemplo, o cosseno de x só é reconhecido pelo programa se for digitado na forma Cos[x] -- expressões como cos[x], cos(x), Cos(x) não serão serão reconhecidas pelo programa.

1. Limites

Limit[f(x), x -> x0] Limite de f(x) quando x tende a x0

Exemplos:

In[1]:= Limit[((x + a)/(x + b))^x, x -> Infinity]

         a - b 
Out[1]= E       


In[2]:= Limit[ (Sec[x] - Sec[a])/(x - a), x->a]

Out[2]= Sec[a] Tan[a]


In[3]:= Limit [ (1 - Cos[a x])/x^2, x-> 0]     
          a
Out[3]=  --  
          2

2. Derivadas

D[f(x), x] Derivada de f(x) com relação a x
D[f(x), {x, n}] Derivada n-ésima de f(x) com relação a x
D[f(x, y, ...), x, y, ...] Derivada de f com relação a x, y, ...

Exemplos:
In[4]:= D[ ArcTan[x] + ArcSin[x], x] 

             1           1
Out[4]= ------------ + ------ 
                  2         2   
        Sqrt[1 - x ]   1 + x

In[5]:= D[ Tan[x], {x, 10}]  

                     10                        8       3
Out[5]= 353792 Sec[x]   Tan[x] + 1841152 Sec[x]  Tan[x]  + 

                  6       5                4       7             2       9 
    1304832 Sec[x]  Tan[x]  + 128512 Sec[x]  Tan[x]  + 512 Sec[x]  Tan[x]

3. Integrais

Integrate[f(x),x] Integral indefinida de f(x) com relação a x
Integrate[f(x),{x,a,b}] Integral de f(x) no intervalo [a, b]

Exemplos:

In[6]:= Integrate [ x^5 Exp[-x^2],x] 

In[7]:= Integrate[ 1/(x*(x^7 + 1)), {x, a, b}]  

                            7                      7  
                   Log[1 + a ]            Log[1 + b ]
Out[7]=  -Log[a] + ----------- + Log[b] - -----------
                        7                      7

In[8]:= Integrate[ 3/(x^2 + 5), {x, -Infinity, Infinity}]

          3 Pi
Out[8]=  -------
         Sqrt[5]

4. Gráficos de funções y = f(x)

Plot [f(x), {x, x_min, x_max}] Gráfico de f(x) no intervalo [x_min, x_max]
Plot[{f1(x), f2(x), ...}, {x, x_min, x_max}] Gráfico de várias funções f1, f2, ...

Exemplos: 

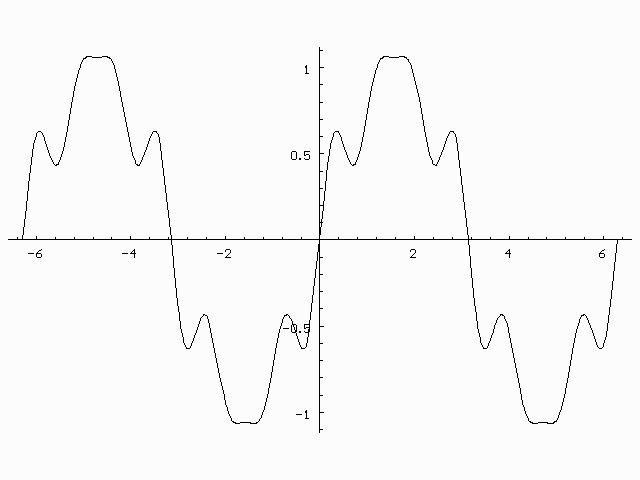
In[9]:= Plot[ Sin[x] + Sin[5x]/5 + Sin[7x]/7, {x, -2*Pi, 2 Pi}]

Out[9]= -Graphics-




5. Gráficos planos em equações paramétricas

ParametricPlot[{f1(t), f2(t)}, {t, t_min, t_max}]
Gráfico de f(t) = (f1(t), f2(t)) com t no intervalo [t_min, t_max]. 
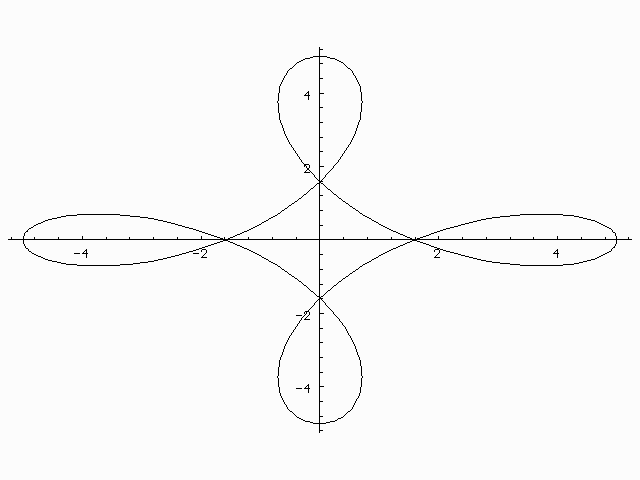
In[10]:= ParametricPlot[{3 Cos[t] + 2 Cos[3t], 3 Sin[t] - 2 Sin[3t]},{t,0,2Pi}]

Out[10]= -Graphics-




6. Gráficos de funções z = f(x, y)

Plot3D[f(x, y), {x, x_min, x_max}, {y, y_min, y_max}, PlotPoints -> Número_de_pontos]
Gráfico de f(x, y) na região [x_min, x_max] X [y_min, y_max]. 

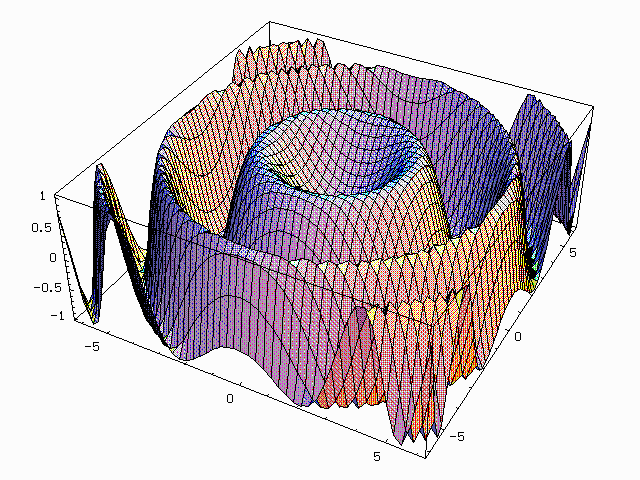
In[11]:= Plot3D[ Sin[(x^2+y^2)/4],{x,-2Pi,2Pi},{y,-2Pi,2Pi},PlotPoints->50]

Out[11]= -SurfaceGraphics-




7. Resolução de equações e sistemas de equações

Solve[equação, variável] ou Solve[{equação1, equação2, ...}, {variável1, variável2, ...}]
Tenta resolver as equações mencionadas com relação às variáveis especificadas. O sinal de igualdade édenotado por = =

Exemplos:

In[12]:= Solve[ 25x^6 + 100x^5 + 301x^4 + 704x^3 + 439x^2 - 1764x - 2205 == 0, x]

                                                7
Out[12]= {{x -> -2 - I}, {x -> -2 + I}, {x -> -(-)}, {x -> -3 I}, {x -> 3 I},
                                                5
                7 
          {x -> -}} 
                5


In[13]:= Solve [ { 3x - 4y == a, x + 2y == b}, {x, y}] 

               a   2 (a - 3 b)       -a + 3 b
Out[13]= {{x -> - - -----------, y -> --------}}
                3       15               10

volta