 O DERIVE é um velho programa de Computação Algébrica elaborado no
Havaí, E.U.A. Ele é o sucessor de um programa ainda mais antigo,
que data do final dos anos 80, chamado MUMATH.
O DERIVE é um velho programa de Computação Algébrica elaborado no
Havaí, E.U.A. Ele é o sucessor de um programa ainda mais antigo,
que data do final dos anos 80, chamado MUMATH.
 O DERIVE é um velho programa de Computação Algébrica elaborado no
Havaí, E.U.A. Ele é o sucessor de um programa ainda mais antigo,
que data do final dos anos 80, chamado MUMATH.
O DERIVE é um velho programa de Computação Algébrica elaborado no
Havaí, E.U.A. Ele é o sucessor de um programa ainda mais antigo,
que data do final dos anos 80, chamado MUMATH.
Uma das coisas que mais chama a atenção no DERIVE é o seu minúsculo tamanho (pouco mais de 200 KB na versão 2.03 de 1990) e enorme "competência": o programa faz um pouco de tudo, desde simplificações algébricas à construção de gráficos de algumas superfícies tridimensionais.
O DERIVE simplifica rapidamente diversos tipos de expressões algébricas, como por exemplo:
6 6 2 2
(x + a ) (x + 1) a x (x + 1)
--------------------------------------- + ---------------------------
6 6 2 2 2 2 4 4 6 6 2 2 2 2
(x + a ) (x - a ) + a x (x - a ) x - a - a x (x - a )
Neste caso, ele mostrará como resposta:
x + 1
---------
2 2
x - a
Expressões algébricas complicadas também podem ser
simplificadas rapidamente pelo DERIVE, como por exemplo:
1 1 1 1
---- + ---- ---- - ----
2 2 2 2
x y x y
------------- - -------------
1 1 1 1
---- - ---- ---- + ----
2 2 2 2
x y x y
-------------------------------------------
2 x + y
---------------------------------------
[ 2 2 ]
[ x + y x - y ] ¦ x y ¦
¦------- + -------¦ ¦---- + ---- - 2¦
[ x - y x + y ] ¦ 2 2 ¦
[ y x ]
que o programa mostra ser equivalente a:
8
- ---------
2 x + y
Ainda como exemplo das suas habilidades, o DERIVE consegue fatorar o polinômio
5
x + x + 1
e mostra como resposta:
2 3 2
(x + x + 1) (x - x + 1)
Cálculo de integrais, limites, derivadas, gradientes, divergentes,
rotacionais, operações com matrizes, vetores, séries de Taylor, séries de Fourier, etc. também podem
ser executados com o DERIVE. Por exemplo, o cálculo da integral de
1/(x4 + 1) com relação a x mostra como resultado:
SQRT(2) ATAN (SQRT(2) x + 1) SQRT(2) ATAN (SQRT(2) x - 1)
---------------------------- + ----------------------------
4 4
2 2
SQRT(2) LN (x - SQRT(2) x + 1) SQRT(2) LN (x + SQRT(2) x + 1)
+ ------------------------------- - -------------------------------
8 8
Aqui, SQRT(2) denota a raiz quadrada de 2.
Além de ser um programa de Computação Algébrica muito bom, o DERIVE também constrói gráficos de funções de 1 ou 2 variáveis.
O DERIVE foi adquirido pela Texas Instruments e tem página própria na Internet de onde é possível se copiar uma versão de demonstração que funciona só por 1 mês. O URL da página do DERIVE é http://www.derive.com
Segue um "manual do usuário" elaborado no Dep. Matemática/UFPB há vários anos. Apesar de bastante desatualizado, este texto de 8 páginas dá uma boa idéia dos recursos do DERIVE.
INFORMACOES BASICAS A RESPEITO DO 'DERIVE - VERSAO 1.59' (18/03/91)
-------------------------------------------------------------------
1. COMO CARREGAR O PROGRAMA E SELECIONAR A OPCAO DESEJADA
Digite DERIVE ao lado do prompt ( A>, B>, [C:\], etc.) do sistema ope-
racional e pressione a tecla [ENTER]. Apos alguns segundos aparecera' a 1a. te-
la do DERIVE com o menu principal na parte inferior do video formado pelas
seguintes linhas:
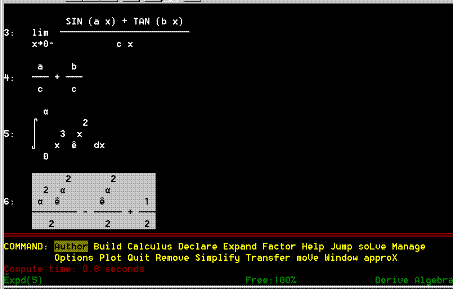
COMMAND: Author Build Calculus Declare Expand Factor Help Jump soLve Manage
Options Plot Quit Remove Simplify Transfer moVe Window approX
Voce se move nesse menu pressionando a tecla TAB ou a barra de espacos. Pressi-
one [ENTER] para selecionar o item que estiver destacado (escrito em video re-
verso). Outra maneira mais rapida de selecionar um item e' pressionar a tecla
que corresponde 'a letra que estiver maiuscula na opcao desejada. Assim, para
selecionar o item "soLve" do menu basta pressionar a letra L.
Para desistir de alguma selecao (feita acidentalmente) pressione a te-
cla ESC.
2. COMO ENTRAR COM AS EXPRESSOES (FUNCOES, MATRIZES, ETC.)
Selecione a opcao AUTHOR do menu principal e digite a expressao dese-
jada. Se sua expressao estiver sintaticamente correta ela sera' escrita em vi-
deo reverso no formato usual da matematica. A sintaxe usada pelo DERIVE e' pa-
recida com a da linguagem BASIC. As expressoes que voce for digitando vao rece-
bendo numeros de acordo com a ordem de entrada e ficando guardadas na memoria.
Voce devera' se referir a uma expressao que foi digitada usando um sinal de #
antes do numero de ordem da expressao. Por exemplo, #3 e' a forma de se refe-
rir 'a terceira expressao digitada. Use as teclas de setas para "passear" pe-
las expressoes digitadas.
As operacoes aritmeticas do DERIVE sao + (soma), - (subtracao), /
(divisao), * (multiplicacao - PODE SER OMITIDO) e ^ (potenciacao). (OBS.: O
simbolo ^ e' o acento circunflexo gerado pelas teclas [Shift] e 6)
As principais funcoes matematicas do DERIVE sao:
x! x fatorial (ou gama de x+1 se x nao for inteiro)
SQRT(x) raiz quadrada de x
EXP(x) ou #e^x exponencial de base e
LOG(x) ou LN(x) logaritmo natural de x
LOG(x, a) logaritmo de x na base a
SIN(x) seno de x
COS(x) cosseno de x
TAN(x) tangente de x
SEC(x) secante de x
COT(x) cotangente de x
CSC(x) cossecante de x
ASIN(x) arco-seno de x
ACOS(x) arco-cosseno de x
ATAN(x) arco-tangente de x
SINH(x) seno hiperbolico de x
COSH(x) cosseno hiperbolico de x
TANH(x) tangente hiperbolica de x
ASINH(x) arco-seno hiperbolico de x
- 1 -
ACOSH(x) arco-cosseno hiperbolico de x
ATANH(x) arco-tangente hiperbolica de x
ABS(x) modulo de x
SIGN(x) sinal de x
MAX(x, y, ...) maximo de x, y, ...
MIN(x, y, ...) minimo de x, y, ...
GAMMA(x) gama de x
PERM(m, p) arranjo de m elementos p a p
COMB(m, p) combinacao de m elementos p a p
Exemplo: Segundo a sintaxe do DERIVE , o logaritmo natural de 2x + 1 devera'
ser escrito como LOG(2*x + 1), LOG(2x + 1) ou LN(2x + 1). A raiz quadrada do
seno de x se escreve como SQRT(SIN(x)) ou SIN(x)^(1/2).
Para conhecer outras funcoes do DERIVE selecione a opcao HELP do menu
e no menu do HELP selecione a opcao FUNCTIONS (ou seja, digite H e F no menu
principal). Aparecera' a 1a. tela de informacoes sobre as funcoes e abaixo um
menu com as opcoes NEXT, PREVIOUS e RESUME. Use a opcao NEXT para mudar para a
proxima tela do help, PREVIOUS para voltar 'a tela anterior e RESUME para sair
do help.
Algumas constantes uteis sao pi (3,14...), #e (2,718...)
#i (unidade imaginaria) e inf (mais infinito).
Algumas letras gregas podem ser geradas pressionando-se a tecla ALT e
uma letra simultaneamente:
ALT A = alfa ALT B = beta
ALT G = gama ALT D = delta
ALT P = pi ALT S = sigma
3. COMO ENCERRAR
Selecione a opcao QUIT do menu e pressione um Y para abandonar as
expressoes digitadas. Se o video estiver com uma luminosidade baixa voce po-
dera' nao perceber que o programa espera a confirmacao de um Y para terminar.
4. COMO OBTER OS RESULTADOS
Quando a expressao desejada estiver destacada na tela (em video rever-
so) selecione a opcao conveniente do menu principal. O calculo de limites, de-
rivadas, integrais, etc. e' feito com a opcao EXPAND.
5. LIMITES
Sintaxe: LIM(u, v, p, l)
onde u e' a expressao que define a funcao
v e' a variavel
p e' o ponto (para o qual v tende)
l e' um numero positivo se o limite for lateral 'a direita e negativo
se o limite for lateral 'a esquerda. l pode ser omitido.
Digite um A para selecionar do menu a opcao AUTHOR, escreva a expres-
sao desejada, pressione [ENTER], pressione um E para selecionar EXPAND do menu
e pressione [ENTER] para que seja feito o calculo indicado.
- 2 -
Exemplos:
LIM(sin(5x)/(bx), x, 0, -1) ---> limite de sen(5x)/(bx) quando
x tende a zero pela esquerda.
LIM( (cos(a + h) - cos(a))/h, h, 0) ---> = -sen(a)
LIM( (1 + 1/x)^x, x, inf) ---> = e
6. DERIVADAS
Sintaxe: DIF(u, v, n)
onde u e' a expressao que define a funcao
v e' a variavel com relacao a qual se quer derivar
n e' a ordem da derivada
Se a funcao tiver mais de 1 variavel entao sera' solicitada uma orde-
nacao das variaveis (ou seja, o DERIVE pergunta qual a primeira, segunda, ...
variaveis. Nesse caso voce pode pressionar [ENTER] para dispensar essa ordena-
cao). O parametro n pode ser omitido.
Exemplos:
2
DIF(ax^2 + bx + c, x) ---> derivada de ax + bx + c com relacao a x
DIF(tan(3x), x, 2) ---> derivada segunda da funcao tg(3x)
DIF(sin(x + 2 exp(y)) atan(xz^2), z) ---> derivada com relacao a z
y 2
de sen(x + 2e ) arctg(xz )
Use a opcao EXPAND do menu para verificar os resultados. Se uma expres-
sao de numero n ja' estiver na tela, entao sua derivada (entre outras possiveis
operacoes) pode ser feita expandindo uma expressao da forma DIF(#n, ...) (Ex.:
DIF(#7, x) ---> derivada da funcao definida pela expressao 7 com relacao a x).
7. INTEGRAIS
Sintaxe: INT(u, x, a, b)
onde u e' a expressao que define a funcao
x e' a variavel de integracao
a e' o limite inferior do intervalo de integracao
b e' o limite superior do intervalo de integracao
a e b podem ser omitidos. E' possivel tambem o calculo de integrais
improprias e integrais multiplas iteradas.
Exemplos:
INT(1/(x^2 + 1), x) ---> integral (indefinida) de 1/(x^2 + 1) com
relacao a x.
- 3 -
INT(sin(u), u, 0, pi) ---> integral do seno no intervalo [0, pi]
INT(1/x^2, x, 1, inf) ---> = 1
INT(INT(-4 x^5 y^2, y, x, 3x), x, 0, 1) ---> integral dupla iterada.
INT(#5, z) ---> integral da 5a. expressao com relacao a z
Para obter os resultados use a opcao EXPAND.
8. COMO DEFINIR UMA FUNCAO
Usando a opcao AUTHOR voce deve escrever a funcao na forma
Nome_da_funcao(variavel1, variavel2, ...) := expressao
Por exemplo, para definir ln(cos(x)) como sendo uma funcao H, digite
o seguinte:
H(x) := ln(cos(x))
Uma funcao tambem pode ser definida usando a opcao DECLARE e no sub-
menu do DECLARE escolhendo a opcao FUNCTION.
Uma vez definida a funcao ela permanecera' na memoria ate' que seja
encerrada a execucao do DERIVE e podera' fazer parte de qualquer outra expres-
sao que vier a ser definida. Diversas formulas de calculo podem ser definidas
dessa forma. A linha abaixo define a formula do comprimento de arco do grafico
de y = f(x), x em [a, b]:
COMPRIMENTO(u, x, a, b) := INT(SQRT(1 + DIF(u, x)^2), x, a, b)
Uma vez digitada essas expressoes (COMPRIMENTO e H), para calcular o comprimen-
to de y = ln(cos(x)) com x no intervalo [0, pi/4] e' so' mandar o DERIVE expan-
dir a expressao COMPRIMENTO(H(x), x, 0, pi/4).
9. DESENVOLVIMENTO EM SERIE DE TAYLOR
Sintaxe: TAYLOR(u, x, a, n) ---> desenvolvimento de Taylor de ordem n da
funcao definida pela expressao u, em torno do ponto x = a.
4 3 2
Exemplo: TAYLOR(exp(x), x, 0, 4) ---> = x /24 + x /6 + x /2 + x + 1
10. SOMATORIOS E PRODUTOS
Sintaxes: SUM(u, n, k, m) ---> somatorio de u com n variando de k ate' m
PRODUCT(u, n, k, m) ---> produto de u com n variando de k a m
k ou m podem ser ilimitados (-inf ou inf).
Exemplos:
SUM(n(n + 1), n , 1, p) ---> soma de p termos da forma n(n + 1)
SUM(1/3^n, n, 1, inf) ---> serie geometrica infinita
- 4 -
PRODUCT(2k, k, 1, r) ---> produto dos r primeiros numeros pares
11. VETORES E MATRIZES
Os vetores devem entrar no formato usual, entre colchetes, com todas
as coordenadas separadas por virgulas (Ex. [1, -3, a]). Uma matriz deve en-
trar como um "vetor de vetores". Dessa forma, a matriz identidade 2 x 2 deve
ser digitada assim: [[1, 0], [0, 1]].
Uma maneira conveniente de trabalhar com vetores e' declara'-los com
a opcao AUTHOR antes de usa'-los. Assim, eles ficarao disponiveis ate o encer-
ramento da secao com o DERIVE. Neste caso use o sinal de atribuicao ( := )
na declaracao. ( Ex.: k := [0, 0, 1] ). O mesmo vale para matrizes.
As operacoes permitidas com vetores sao: soma, produto por escalar,
produto interno (todas com notacao usual) e produto vetorial (CROSS).
As operacoes com matrizes sao soma, produto, produto por escalar, de-
terminantes, inversa e potencias (todas com notacao usual) e A` para a matriz
transposta (OBS.: a transposta e' indicada com um acendo grave; nao confundir
com apostrofo. No papel, o acento grave pode ser impresso como uma barra verti-
cal).
Exemplos:
Use a opcao AUTHOR (ou seja, pressione um A) para declarar o seguinte:
v := [1, b, -3] (pressione [ENTER] e A)
w := [-5, 2, z] ([ENTER] e A)
M := [[1, -2], [3, 0]] ([ENTER] e A)
N := [[a, b + 1], [-7, d/2]] ([ENTER])
Agora calcule o seguinte (use a opcao EXPAND):
v + w ---> soma dos vetores v e w
(2v).w ---> produto interno de 2v com w
CROSS(v, w) ---> produto vetorial v x w
M - 3N ---> matriz M menos o produto escalar de 3 por N
M.N ---> produto de M por N
M^-1 ---> matriz M elevada a -1, ou seja, e' a inversa de M
DET(N) ---> determinante da matriz N
(M`)^2 ---> o quadrado da matriz transposta de M
Use a opcao AUTHOR para definir a seguinte expressao que define o
produto misto dos vetores a, b, c :
PROD_MISTO(a, b, c) := a . CROSS(b, c)
Agora entre com a expressao PROD_MISTO(v, w, [2, -1, 3]) atraves da
opcao AUTHOR e use a opcao EXPAND para calcular o produto misto de v, w e
[2, -1, 3].
12. GRADIENTE, DIVERGENTE, ROTACIONAL E LAPLACIANO
Sintaxes: GRAD(expressao) ---> gradiente
DIV(vetor) ---> divergente
CURL(vetor) ---> rotacional
- 5 -
LAPLACIAN(expressao) ---> laplaciano
Exemplos:
2 z 2 z z 2 z
GRAD(x y^2 #e^z) ---> gradiente de x y e = [ y e , 2xye , xy e ]
DIV( [x + y, y cos(x), 5z] ) ---> = 6 + cos(x)
13. POLINOMIO CARACTERISTICO E AUTOVALORES DE UMA MATRIZ
Sintaxes: CHARPOLY(A, v) ---> polinomio caracteristico de A na variavel v
EIGENVALUES(A) ---> autovalores da matriz A
Exemplos:
A := [[2, 3], [a, b]] ( matriz declarada com a opcao AUTHOR)
2
CHARPOLY(A, x) ---> x + x(-b - 2) - 3a + 2b
EIGENVALUES(A) ---> autovalores de A = 2 e b
14. OS ARQUIVOS *.MTH
O disquete do DERIVE contem 17 arquivos com extensao .MTH (COORD.MTH,
INTEGRAL.MTH, DERIV.MTH, PLOT3D.MTH, etc.) . Esses arquivos contem diversas
formulas e exemplos interessantes. Voce podera' ampliar seus conhecimentos so-
bre o DERIVE lendo e testando esses arquivos bem como observando as informacoes
das telas do help. Todos os .MTH e o help (DERIVE.HLP) podem ser impressos em
papel (ligue a impressora e digite A> COPY Nome_do_arquivo.extensao PRN: e
pressione [ENTER].)
Voce pode carregar e testar os arquivos .MTH atraves da opcao TRANSFER
do menu. O TRANSFER contem um sub-menu com as opcoes
TRANSFER: Merge Clear Demo Load Save Print sTate
como sempre, voce se move no TRANSFER com TAB ou barra de espacos e escolhe com
[ENTER] ou pressionando a letra que estiver em maiusculas.
A opcao MERGE permite que voce mescle (ou misture) suas expressoes com
as expressoes de um arquivo .MTH do disco cujo nome sera' solicitado. A opcao
LOAD carrega um arquivo .MTH do disco mas retira da memoria todas as suas ex-
pressoes digitadas antes do LOAD. A opcao SAVE permite que voce crie o seu pro-
prio arquivo de formulas e funcoes prediletas (e nesse caso voce devera'
fornecer o nome do arquivo que sera' criado e dizer o que ira' usar o arquivo:
se for o proprio DERIVE sera' criado um arquivo .MTH, se for o BASIC sera' cri-
ado um arquivo .BAS, se for o Pascal um .PAS ou se for o FORTRAN um .FOR - cada
arquivo sera' criado usando a sintaxe da respectiva linguagem).
Agora use a opcao TRANSFER MERGE (isto e', pressione T e M) para car-
regar do disco o arquivo COORD.MTH (nao precisa digitar o .MTH). Este arquivo
habilita o DERIVE a calcular jacobianos de transformacoes. Quando todas as ex-
pressoes do COORD.MTH aparecerem na tela use a opcao AUTHOR para entrar com a
seguinte expressao:
JACOBIAN( [u^3, cos(u + v^2)], [u, v] )
Para calcula'-la use a opcao EXPAND. Sem o arquivo COORD.MTH nao e'
possivel o calculo uma vez que a formula do jacobiano esta' no arquivo.
Ha' uma forma de carregar o arquivo .MTH e verificar a execucao auto-
- 6 -
matica das operacoes sendo feita 'a medida que voce pressiona uma tecla. Bas-
ta usar a opcao DEMO do sub-menu do TRANSFER.
Carregue (com TRANSFER MERGE, TRANFER LOAD ou TRANSFER DEMO) outros
arquivos .MTH e divirta-se com as formulas e funcoes contidas neles.
Voce pode acrescentar linhas de comentarios 'as suas formulas ou fun-
coes. Para fazer isso use a opcao AUTHOR e digite o comentario entre aspas.
15. EXPRESSOES ALGEBRICAS
As expressoes algebricas tem a sintaxe usual. E' possivel diversos
tipos de fatoracao e simplificacao. Entre com a expressao (x + 2y + 1)^3 (use a
opcao AUTHOR). Expanda essa expressao com relacao a x e depois com relacao a y:
(1.) Pressione E X [ENTER] para expandir com relacao a x
(2.) Pressione E Y [ENTER] para expandir com relacao a y
Nos dois casos acima (e em todos os outros) voce precisara' responder
qual o numero da expressao que sera' expandida. Veja na tela o numero que cor-
responde 'a expressao que voce quer e digite # seguido do numero quando o
DERIVE perguntar qual o numero da expressao. Observe que as respostas encontra-
das acima sao aparentemente diferentes.
Entre com a expressao (x^2 + 2xy + y^2)/(x^2 - y^2) e simplifique-a
usando a opcao SIMPLIFY do menu.
Entre com a expressao x^4 - x^3 + 3x^2 - 4x - 4 e fatore-a usando a
opcao FACTOR do menu. FACTOR tem um sub-menu formado pelas opcoes Trivial,
Squarefree, Rational, raDicals, Complex. Use cada uma dessas opcoes e compare
as respostas encontradas.
Carrege o arquivo ALGEBRA.MTH ( digite T L ALGEBRA [ENTER] Y ), use as
setas para cima ou para baixo para selecionar (destacar) alguma expressao que
seja do seu interesse. Depois pressione S (para simplificar) ou E (expandir).
16. EQUACOES, INEQUACOES E SISTEMAS
Equacoes e inequacoes entram no formato usual, sendo que /= e' usa-
do como sinal de diferente, <= como menor ou igual e >= como maior ou igual.
Os sistemas entram de modo semelhante aos vetores: as equacoes separa-
das entre si por virgulas e colchetes envolvendo todas as equacoes.
Por exemplo, o sistema
x - 3y = 1
5x + y = 0
devera' entrar na forma [x - 3y = 1, 5x + y = 0].
Uma vez que a equacao ou sistema que voce quer resolver esteja na te-
la voce deve usar a opcao SOLVE para obter sua solucao.
Os sistemas indeterminados terao os simbolos @1, @2, ... na solucao
identificando as variaveis livres. Desse modo, a solucao do sistema
[x - y = 0, 2x - 2y = 0] sera' [x = @1, y = @1], ou seja, y = x.
17. GRAFICOS
A forma de entrar com a funcao para se construir um grafico e' a mes-
ma vista acima (geralmente via opcao AUTHOR). Suponhamos que voce queira cons-
truir o grafico de f(x) = x^2 sen(x). Entao voce podera' entrar com as seguin-
tes expressoes, equivalentes sob o ponto de vista da construcao de graficos:
y = x^2*sin(x), z = u^2 sin(u) ou, simplesmente, x^2 sin(x).
Quando a funcao tiver sido definida sera' necessario colocar a tela
- 7 -
no modo grafico. Isto e' feito com a opcao OPTIONS. No sub-menu de OPTIONS voce
devera' escolher a opcao DISPLAY. O DISPLAY por sua vez tem 3 sub-menus: Mode,
Resolution e Adapter. Dentro de cada sub-menu voce se move com a barra de espa-
cos e para mudar de sub-menu voce usa a tecla TAB. Escolha em MODE a opcao
GRAPHICS, em RESOLUTION escolha HIGH e em ADAPTER escolha CGA. Uma forma rapida
de fazer isso e' pressionar as teclas O (Options), D (Display), G, H, C e
[ENTER]. Estando definida a funcao e a tela no modo grafico use a opcao PLOT
para ter acesso ao seguinte menu:
COMMAND: Algebra Center Delete Help Move Options Plot Quit Scale Ticks Window
Zoom
Use o PLOT para dar inicio 'a construcao do grafico e use a opcao
ALGEBRA para entrar com novas equacoes.
Use a opcao SCALE para mudar a escala do grafico. (No SCALE voce pre-
cisara' usar a tecla TAB)
Cada vez que voce entrar com uma nova equacao para construir um gra-
fico serao construidos todos os outros graficos anteriores. Para ser construi-
do so' o grafico da ultima equacao fornecida voce devera' pressionar as teclas
D e B (de DELETE BUTLAST).
Graficos em equacoes parametricas podem ser construidos por um pro-
cesso semelhante, so' que voce entra com a equacao na forma de vetor (Ex.:
[sin(3t), sin(4t)] ). Graficos em coordenadas polares sao feitos usando-se a
opcao OPTIONS TYPE POLAR. Uma vez feito esse ajuste as equacoes podem entrar
de modo semelhante ao das funcoes y = f(x). Os graficos de funcoes z = f(x, y)
tambem podem ser construidos de forma semelhante.
Os arquivos PLOT2D, PLOT3D e PLOTPARA contem diversas equacoes que
podem ser usadas na construcao de graficos.
A opcao OPTIONS DISPLAY permite que se coloque a tela novamente no
modo texto.
18. OPERACOES COM NUMEROS COMPLEXOS
E' possivel a simplificacao de expressoes que envolvem numeros comple-
xos, bem como o calculo de funcoes com argumentos complexos. A unidade imagina-
ria devera' entrar como #i ou pressionando-se as teclas [Alt] [i]. Na tela, o
i devera' aparecer com um acento circunflexo.
Exemplos: (1 + #i)^10 ---> = 32i (OBS.: (1 + i)^10 sera' tratado como um
polinomio de grau 10 na variavel i)
LOG(-1) ---> = i.pi
SINH(#i x) ---> = i sen(x)
Este texto esta' gravado no disco sob o nome de DERIVE.DOC. Para
lista'-lo na tela digite A> TYPE DERIVE.DOC. Para "congelar" um trecho na tela
pressione as teclas Ctrl (= CONTROL) e S simultaneamente.
- 8 -