The aim of this paper is to investigate the blowup behavior of solutions to
the Brezis-Nirenberg equation with the Robin condition. In our previous paper
Kabeya, Yanagida and Yotsutani [10],
we proved the range of ![]() for which a
unique positive radial solution to
for which a
unique positive radial solution to
When ![]() , in the three dimensional case, a solution to
(1.1)
exists for
, in the three dimensional case, a solution to
(1.1)
exists for ![]() while in the higher dimension, a solution does for
while in the higher dimension, a solution does for ![]() (see e.g.,
Brezis and Nirenberg [4],
Brezis and Peletier [5],
or [10]).
In this sense, the three dimensional case is an exceptional case and interesting
phenomena occur in this case. So we concentrate on the three dimensional case.
(see e.g.,
Brezis and Nirenberg [4],
Brezis and Peletier [5],
or [10]).
In this sense, the three dimensional case is an exceptional case and interesting
phenomena occur in this case. So we concentrate on the three dimensional case.
Since our concern is on radial solutions, we consider the initial value
problem of the ordinary differential equation
We introduce three numbers. Let ![]() be defined by
be defined by
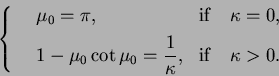
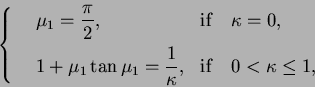
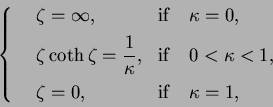
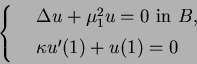
Let us recall our previous results (see also [4]
for ![]() ).
).
Theorem A.(Theorem 1.1 of [10])
Let ![]() and
and ![]() . If
. If ![]() , then (1.1)
has a unique radial solution. If
, then (1.1)
has a unique radial solution. If ![]() , then (1.1)
has no radial solution.
, then (1.1)
has no radial solution.
By Theorem A, a mapping from ![]() to the initial
value
to the initial
value ![]() is defined, that is,
is defined, that is, ![]() is a function
of
is a function
of ![]() . Let us denote the unique solution by
. Let us denote the unique solution by ![]() . We can draw the graph of
. We can draw the graph of ![]() . Concerning the graph of
. Concerning the graph of ![]() , we have the following global behavior.
, we have the following global behavior.
Theorem B. ((i) of Theorem 1.3 of [10])
Let ![]() . Then the graph of
. Then the graph of ![]() is a continuous curve satisfying
is a continuous curve satisfying ![]() as
as ![]() and
and ![]() as
as ![]() .
.
We can see that ![]() is the blowup point.
is the blowup point.
The purpose of this paper is to show the blowup order of ![]() and an asymptotic behavior of a rescaled solution mainly
following the method by Brezis and Peletier [5].
We utilize the Green function as in [5]
and Rey [13]
used for the Dirichlet problem.
and an asymptotic behavior of a rescaled solution mainly
following the method by Brezis and Peletier [5].
We utilize the Green function as in [5]
and Rey [13]
used for the Dirichlet problem.
First we consider the case ![]() .
.
The blowup rate of
In Theorem 1.1,
we exclude the case ![]() . In this
case, we see a different blowup order. Note that
. In this
case, we see a different blowup order. Note that ![]() when
when ![]() . The difference is affected by whether
. The difference is affected by whether ![]() or not.
or not.
Similar to [5], the limiting behavior of a scaled function is obtained. Let us denote the Green function of
In [10],
the differential form of the Pohozaev identity plays a crucial role. However, to
investigate the blowup nature, we need to use the integral form of the identity
because it enables us to treat the Dirac ![]() function-like
behavior.
function-like
behavior.
As related topics, for the Neumann problem (![]() ), such a blowup behavior of solutions to the scalar-field equation
with the critical Sobolev exponent is discussed in Budd, Knaap and Peletier [6]
and there are many works on the nearly critical growth (see, e.g., Atkinson and
Peletier [2],
Han [8]
or Pan and Wang [12]).
), such a blowup behavior of solutions to the scalar-field equation
with the critical Sobolev exponent is discussed in Budd, Knaap and Peletier [6]
and there are many works on the nearly critical growth (see, e.g., Atkinson and
Peletier [2],
Han [8]
or Pan and Wang [12]).
What will happen in the case where ![]() ? For
? For ![]() , the unique
existence of a solution was also discussed in [10].
Moroever, similar results to Theorems 1.1
and 1.3
are obtained (the blowup rate is as in Theorem 1.1).
The blowup point is a continuous function of
, the unique
existence of a solution was also discussed in [10].
Moroever, similar results to Theorems 1.1
and 1.3
are obtained (the blowup rate is as in Theorem 1.1).
The blowup point is a continuous function of ![]() . These will
be discussed in a forthcoming paper [9].
. These will
be discussed in a forthcoming paper [9].
This paper is organized as follows. The Pohozaev identity for an auxiliary inhomogeneous linear problem is discussed in Sections 2 and 3. In Section 4, several properties of the accurately approximate solution, which are useful for proofs of Theorems 1.1, 1.2 and 1.3, are proved. Proofs of Theorem 1.1, 1.2 and 1.3 are given in Section 5.